Thermodynamique chimique. Second principe de la thermodynamique Etat d'équilibre pour une réaction entre gaz parfaits

Nous avons vu au paragraphe précédent que l'enthalpie libre d'un système dans lequel la transformation X à P se produit a pour expression :
G = ( 1-x ).( µ°_X + R.T ln (a_X) ) + x . (  µ°_P + R.T ln (a_P) )

Nous allons à présent étudier la variation de G en fonction de x suivant l'état physique de X et P et en tirer  les conséquences quand à l'évolution du système .

Cas 1 : X et P sont des gaz parfaits. Transformation à pression constante p = 1 bar.

Pour un gaz parfait, l'activité est définie comme le rapport de sa pression partielle à la pression de référence p° = 1 bar.

Nous avons donc a_X = p_X /p° = g_X . p_t / p° où g_X est la fraction molaire de X dans le mélange gazeux et p_t la pression totale des gaz dans le mélange. Cette pression étant constante et égale à p° = 1 bar, il vient :

a_X = g_X = n_X / (n_X + n_P) = (1 - x ) / 1   et de même a_P = x / 1

L'expression de G devient donc G = (1 - x).(µ°_X + R.T ln (1 - x) ) + x . (   µ°_P + R.T ln (x) )

soit G - µ°_X  = x . D_rG° + (1 - x). R.T ln (1 - x) + x . R.T ln (x)

ou encore si T = 298K : G - µ°_X  = D_rG°. x  + 2493 . ((1 - x). ln (1 - x) + g . ln (x) )

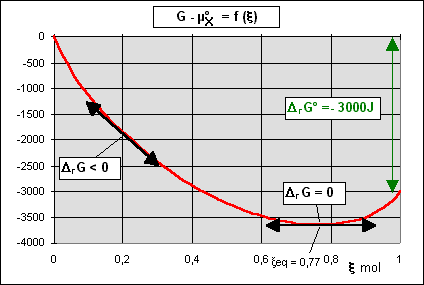Dans le cas où DrG°vaut - 3000 J.mol-1, la courbe ci-contre (en rouge) représente les variations de G - µ°X en fonction de l'avancement x de la réaction X (gaz) à P (gaz) . La pente de la tangente à cette courbe représente DrG puisque par définition DrG = dG/dx . Lorsque  x = 0, DrG est négatif donc la réaction X (gaz) à P (gaz) va se produire et x va croître. Cette réaction va se poursuivre jusqu'à ce que G soit minimum, c'est à dire jusqu'à ce que x = xeq et DrG = 0.

x_eq = 0,77 mol correspond donc à l'avancement de la réaction à l'équilibre, la composition du système étant alors de 0,77 mol de P et 0,23 mol de X.

Notez bien sur ce graphique la différence qu'il y a entre G du système, D_rG et D_rG°.

Position de l'état d'équilibre suivant la valeur de D_rG°

L'animation ci-dessous vous permet de faire varier l'enthalpie libre standard D_rG° de la réaction et de visualiser l'influence de cette variation sur la forme de la courbe G = f(x) . Elle vous permet également de constater l'influence de cette variation sur la position d'équilibre.

Conclusions.

Lorsqu'une transformation du type  X à P se déroule dans un système à température constante, la transformation s'arrète lorsque l'avancement de réaction est tel que l'enthalpie libre du système atteint la valeur la plus faible possible.

Lorsque la transformation X à P se produit en phase homogène, cette valeur de G correspond à un minimum, c'est à dire à la valeur de x = x_eq telle que dG/dx = D_rG = 0 .

La valeur de x_eq dépend de D_rG° : plus D_rG° est négative et plus la valeur de x_eq est proche de la valeur maximale qui correspond à un taux d'avancement de réaction de 100% . Au contraire, plus D_rG° est positive et plus x_eq  est faible et proche de zéro. 

SIMULATEUR

Vous trouverez la simulation suivante dans la section simuler. Pour y accéder, cliquez sur l'icône dans le bandeau de gauche et choisissez le chapitre correspondant dans la table des matières. Ces simulations sont toujours interactives.

Thermodynamique chimique. Second principe de la thermodynamique Etat d'équilibre pour une réaction entre gaz