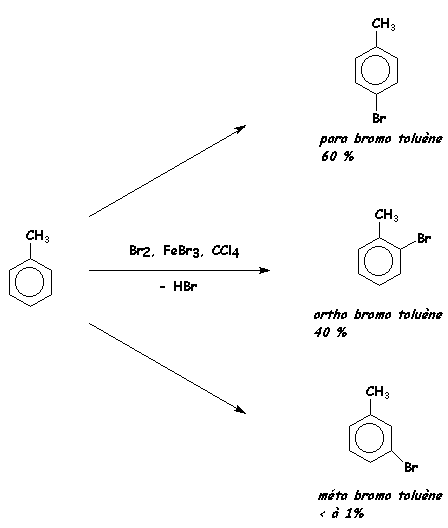
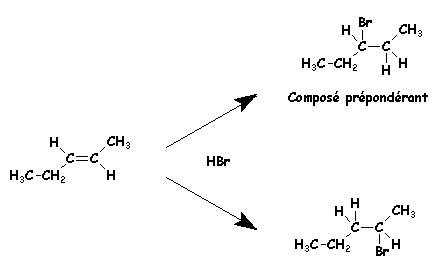
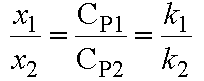Les réactions parallèles sont constituées
de deux réactions, ou plus, ayant les mêmes réactifs mais conduisant à des
produits différents.
On parle de réactions jumelles lorsque tous les réactifs sont les mêmes. Par
exemple :
|
A
|
|
P1
|
|
| et |
A
|
|
P2
|
| ou |
A + B
|
|
P1
|
|
A + B
|
|
P2
|
Lorsque seulement un réactif est commun, on parle de réactions compétitives. Par exemple :
|
A + B
|
|
P1
|
|
| et |
A
|
|
P2
|
| ou |
A + B
|
|
P1
|
|
A + C
|
|
P2
|
Très souvent une des réactions est
sensiblement plus rapide que les autres et conduit à des produits dits majoritaires,
les autres réactions peuvent alors être considérées comme des réactions secondaires.
La proportion des produits formés dépend
de la vitesse relative des diverses réactions parallèles et n'est pas dans
un rapport simple.
On ne peut donc pas écrire une équation bilan classique pour l'ensemble des
réactions.
5.3.1 Réactions parallèles jumelles d'ordre 1.
D'une manière générale, chacune des réactions peut avoir un ordre quelconque et faire intervenir plusieurs réactifs et produits, cependant, pour simplifier nous nous limiterons à l'étude de réactions parallèles qui sont toutes d'ordre 1.
On peut les schématiser par :
|
A
|
|
P1
|
|
| et |
A
|
|
P2
|
|
généralisable à n réactions...
|
|||
a) Approche qualitative.
Avant d'aborder dans le détail l'étude analytique de la loi de vitesse, il est utile de se familiariser avec le comportement qualitatif du système cinétique.
Dans un premier temps, nous nous limiterons au cas de deux réactions.
|
A
|
|
P1
|
|
| et |
A
|
|
P2
|
La réactif A est consommé simultanément
par les deux réactions.
Il est donc facile de comprendre que sa vitesse globale de disparition sera
la somme des vitesse des deux réactions.
Par contre, chaque produit (ici P1 et P2) est formé avec la vitesse propre
de sa réaction.
La proportion des produits formés sera donc dans le rapport de ces vitesses,
donc des valeurs des coefficients de vitesse.
b) Etude analytique de la loi de vitesse.
Soit le cas simple
|
A
|
|
P1
|
|
| et |
A
|
|
P2
|
Toutes les deux réactions sont
d'ordre un et de coefficients de vitesse respectifs k1 et
k2.
Les lois de vitesse de chaque réaction considérée séparément s'écrit :
v1 = k1 . CA et v2 = k2 . CA
La vitesse globale de disparition de A est la somme de ces deux vitesses, puisque A est consommé simultanément par ces deux réactions.
v = - dCA / dt = v1 + v2 = k1 . CA + k2 . CA = (k1 + k2) . CA
En notant kobs = k1 + k2 , il vient :
v = - dCA / dt = kobs . CA
qui a la forme d'une loi de vitesse du premier ordre de coefficient de vitesse kobs , laquelle s'intègre facilement en :
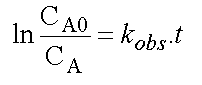
D'où l'expression de la variation de CA en fonction du temps :
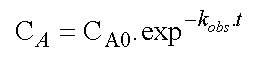
La variation de A en fonction du
temps se fait donc en suivant une loi du premier ordre dont le coefficient
de vitesse est la somme des coefficients de vitesses des réactions jumelles.
Ce résultat est généralisable aux cas où il y a plus de deux réactions jumelles
(toutes du même ordre).
Exprimons maintenant les concentrations des produits P1 et P2 en fonction du temps.
Soient x1
et x2 les concentrations de P1 et P2
formées à un instant t.
Et x la concentration de A transformée au même instant.
La stúchiométrie des réactions montre
que x = x1 + x2.
Les concentrations des différentes espèces
sont donc :
|
A
|
P1
|
P2
|
|
|
t = 0
|
CA0
|
0
|
0
|
|
t
|
CA0 - x CA0 - (x1 + x2) |
x1
|
x2
|
Ceci pour des concentrations initiales en P1 et P2 nulles.
Les vitesses de chaque réactions s'écrivent :
v1 = dx1 / dt = k1 . CA et v2 = dx2 / dt = k2 . CA
En faisant le rapport il vient
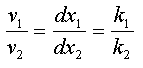
Au temps t =O, on a x1 = x2 = 0, d'où
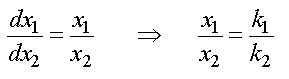
En tenant compte de la relation x = x1 + x2 , il vient :
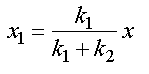 et
et
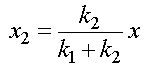
Or CA = CA0 - x d'où x = CA0 - CA et
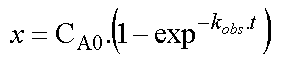
avec kobs = k1 + k2 d'où en définitive :
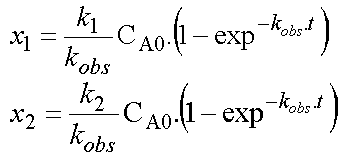
c) Influence des valeurs des coefficients de vitesse sur le régime cinétique.
Voyons de nouveau quelques situations typiques.
d) Remarques sur l'état final.
Lorsque la réaction est terminée,
c'est à dire lorsque le réactif est entièrement consommé, on obtient un mélange
des produits dans des proportions qui dépendent du rapport des coefficients
de vitesse des réactions paralèles.
Ce mélange ne doit pas être confondu avec celui obtenu par un système de réactions
opposées qui conduit à un état d'équilibre. Dans le cas présent, les réactifs
étant épuisés, il n'y a plus aucune transformation dans le système.
|
Simulateur
|
e) Traitement des données expérimentales.
L'objectif est double :