1. (i) Pour x = 0 on a
Si f(0) =1, alors :
ce qui est exclu car f n'est pas constante , donc f(0)=0. 2pts
Réciproquement, s'il existe a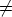 
0
tel que f(a) = 0, alors :
, ce qui est exclu car f n'est pas constante. 1pt
(ii) Pour x > 0, on a 
. 1pt
2. On a
et 
d'où 
.
Pour étudier la fonction au voisinage de 1 on pose h =x -1, on étudie f(1+h) au voisinage de 0.
On écrit :
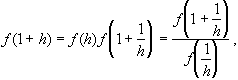
, on a donc :
; la fonction est continue au point 1. 2pts
Soit 
d'où 
et la
fonction est continue en x0. 2pts
3. Pour tout x réel, on a 
et g(x) est défini.
On a alors les égalités successives :
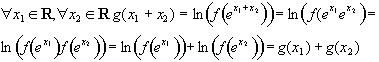
2pts
La fonction g est continue en tout point de R comme composée des fonctions :
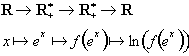
1pt
4. L'application est donc définie par 
.
D'où, en posant, 
. 2pts
On a donc l'expression de f pour x > 0, 
.
Pour x < 0, on a
avec 
d'où 
ou 
.
Donc pour x<0,
si
alors 
et si alors 
. 2pts