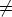Arithmétique PGCD et PPCM Propriété du pgcd

précédent

 suivant résumé résumé

Propriété du pgcd :

Soient deux entiers non nuls appartenant à N. Si un entier positif d est tel que les deux propriétés suivantes soient vérifiées : alors d est le plus grand commun diviseur de ces deux entiers, d = pgcd(a,b).


Démonstration :

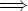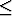D'après la propriété (c | d et d 0) implique c inférieur ou égale d , si un entier d vérifie les deux propriétés précédentes, il est plus grand que tous les diviseurs communs c de a et b et c'est le pgcd(a,b). On cherche donc un plus grand diviseur commun d au sens tout autre diviseur commun de a et b est un diviseur de d, notion qui entraîne que d est aussi plus grand, (au sens de la relation d'ordre), que tout diviseur commun.