|
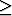 b, et divisons a par b : a = bq1 + r1 avec 0
b, et divisons a par b : a = bq1 + r1 avec 0
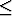 r1 < b.
r1 < b.
Tout diviseur commun à a et b est un diviseur
commun à b et r1 et réciproquement.
Donc pgcd(a,b) = pgcd(b,r1).
On itère le procédé et l'on sait que la suite des restes obtenue
est une suite d'entiers strictement décroissante. Donc à un
certain stade rk = 0.
Cet algorithme est une démonstration d'existence du pgcd. Il
permet aussi de montrer que tout diviseur commun à a et b est
un diviseur de d. Comme nous l'avons vu sur l'exemple, cet
algorithme permet de déterminer successivement chaque reste comme
na + mb avec n et m entiers. Nous allons donc nous intéresser
aux entiers qui peuvent s'écrire sous la forme ax + by.
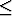 r2 < r1
r2 < r1 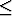 r3 < r2
r3 < r2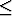 rk-1 < rk-2
rk-1 < rk-2