En mathématiques, on se situe dans le cadre d'une logique à deux
valeurs. Une proposition mathématique "P" est soit vraie soit
fausse. Si elle est vraie, nous lui attribuons la valeur 1, (ou V) ; si elle est fausse, nous lui attribuons la valeur logique 0,
(ou F).
On peut trouver des propositions toujours vraies, par
exemple "x 2 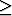 0" pour x réel, ou "0 = 0" qu'on appelle
des tautologies, des propositions toujours fausses, par exemple
"0 = 1" et des propositions tantôt vraies, tantôt fausses, par
exemple "x 2 = 1" qui est vraie pour "x = 1" ou "x = - 1", et
fausse sinon.
0" pour x réel, ou "0 = 0" qu'on appelle
des tautologies, des propositions toujours fausses, par exemple
"0 = 1" et des propositions tantôt vraies, tantôt fausses, par
exemple "x 2 = 1" qui est vraie pour "x = 1" ou "x = - 1", et
fausse sinon.
But de ce chapitre
On examine comment, à partir de
propositions données en former de nouvelles, à l'aide de
connecteurs logiques :
- la négation --- le "non"
- la conjonction --- le "et"
- et la disjonction logique --- le "ou".
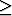 0" pour x réel, ou "0 = 0" qu'on appelle
des tautologies, des propositions toujours fausses, par exemple
"0 = 1" et des propositions tantôt vraies, tantôt fausses, par
exemple "x 2 = 1" qui est vraie pour "x = 1" ou "x = - 1", et
fausse sinon.
0" pour x réel, ou "0 = 0" qu'on appelle
des tautologies, des propositions toujours fausses, par exemple
"0 = 1" et des propositions tantôt vraies, tantôt fausses, par
exemple "x 2 = 1" qui est vraie pour "x = 1" ou "x = - 1", et
fausse sinon.