La proposition Si
"P" alors "Q" ne dit pas que l'hypothèse "P" est
vraie ; elle dit seulement que si l'hypothèse "P"
est vraie, alors la conclusion "Q" l'est aussi. Ceci s'exprime
donc à l'aide des symboles de conjonction et de disjonction par
l'une ou l'autre des phrases suivantes:
--- "(non P) ou Q"
--- "non (P et (non Q))"
Les formules suivantes sont donc équivalentes :
--- "P 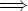 Q"
Q"
--- "(non P) ou Q"
--- "non (P et (non Q))"
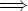 Q"
Q"