|
|
 |
|
|
|
Considérons une grandeur physique représentée par une fonction scalaire s se propageant dans une direction repérée par un axe Oz. Cette grandeur s peut se mettre sous la forme:
où les paramètres qui caractérisent l'onde sont:
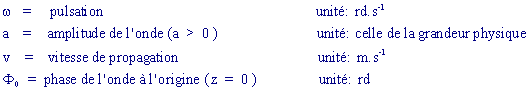
Ce paramètre dépend de la manière dont on
choisit l'origine des temps: le plus souvent on prendra: 
L'onde est dite sinusoïdale, se propageant
suivant l'axe Oz, dans le sens des valeurs croissantes de z . En effet le point M repéré
par sa côte z est atteint par l'onde après
être passé par le point origine z = 0, c'est-à-dire avec un retard: 
. Si l'on exprime s sous la forme: 
l'onde sinusoïdale progressive se
déplace dans le sens des valeurs décroissantes de z.
On définit aussi les grandeurs suivantes:
T = période temporelle.
C'est l'intervalle de temps le plus court pour lequel le phénomène se reproduit identiquement à lui-même en un point M0 donné : s ( t + T , M0 ) = s ( t , M0 ).
Cette relation se traduit, dans le cas d'une onde sinusoïdale, au point M0, repéré par sa côte z0, par:
Cette égalité n'est
vérifiée que si: 
; 
l période spatiale ou longueur d'onde.
Soient M et M' deux points de côtes z et z' atteints par l'onde à l'instant t0. Leurs états vibratoires seront représentés par :
Appelons l
la plus courte distance qui sépare M et M' telle que: 
en remplaçant s par
son expression: 
on en déduit :
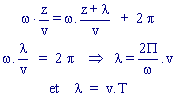
La longueur d'onde dépend de la vitesse de propagation dans le milieu.
Lorsque la grandeur
physique qui se propage est vectorielle, l'onde associée est sinusoïdale progressive
dans la direction Oz si chaque composante sx, sy et sz de la grandeur vectorielle
S s'écrit : 
|
|
|
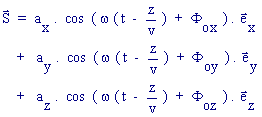
