|
 E.3.
Théorème de la quantité de mouvement
pour
un point
pour
un système de points matériels
pour
un système isolé
 E.3.1.
pour un point
En mécanique classique, la
masse est constante en fonction du temps, on a donc, par rapport à
un référentiel galiléen:
|
|
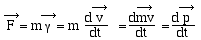
Théorème
de la quantité de mouvement pour un point matériel
Dans un référentiel
galiléen, la résultante des forces appliquées
à un point matériel est égale à
la dérivée par rapport au temps du vecteur quantité
de mouvement :
|
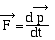
E.3.2.
pour un système matériel
Par définition la quantité
de mouvement du système de N points matériels dans le
référentiel [R] est la somme (vectorielle) des quantités
de mouvement de chacun des points matériels du système:
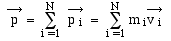
Or, 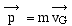 car
la quantité de mouvement d' un système matériel
dans un référentiel R est égale à la quantité
de mouvement d' un point matériel G confondu avec le centre de
masse du système où serait concentrée toute la
masse du système.
Dérivons la relation précédente
par rapport au temps
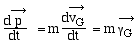
En tenant compte du théorème
du centre d' inertie:
|
|
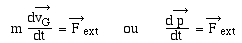
Théorème
de la quantité de mouvement
Dans un référentiel
galiléen la résultante des forces extérieures
à un système est égale à la dérivée
par rapport au temps de la quantité de mouvement du système.
|
Faire les exercices :
 Ecrire
l'équation fondamentale
Point matériel libre
Point matériel dans un champ uniforme
Marcheur sur
une plate-forme mobile.
Marcheur sur
un plateau mobile (cas limites)
Du plateau
mobile à la fusée.
E.3.3.
pour un système isolé.
Un système est isolé s'
il n' est soumis à aucune force extérieure, soit  ,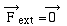
par suite:
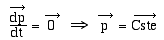
La quantité
de mouvement d' un système mécanique isolé
est constante.
Faire les exercices :
 Jet de briques
Neutron contre noyaux
Le
choc était comment?
|
