|
1°) Le référentiel
R par rapport auquel le mouvement de M est plus simple est, par rapport à
G, en rotation uniforme autour de Oz avec la vitesse angulaire w. Les origines des deux référentiels
sont confondues. Le mouvement de M dans ce référentiel est alors rectiligne
uniforme.
On peut choisir comme base de G, la base cartésienne
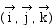 mais on peut également choisir dans les deux référentiels la
même base cylindrique.
mais on peut également choisir dans les deux référentiels la
même base cylindrique.
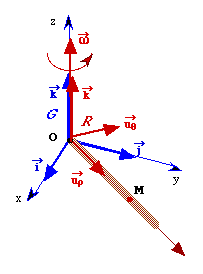
2°) La vitesse de M pour R est égale à
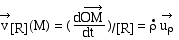
Pour un observateur lié au référentiel
R, G tourne avec une vitesse angulaire de rotation telle que :
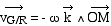
La vitesse de M par rapport au référentiel
G est alors la somme de la vitesse de M par rapport à R (la tige) et de la
vitesse de la tige (R) par rapport à G; cette dernière est l'opposée
de la vitesse de G par rapport à R exprimée précédemment
:
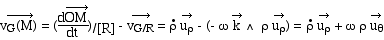
Avec les données, 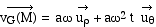
Nous retrouvons bien la règle de composition
des vitesses lorsque les origines O et O1 des référentiels restent
confondues :
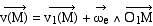
Entre l'instant initial et un instant t donné,
la trajectoire de M par rapport au référentiel R est la portion de
droite qui porte le vecteur de base  . .
Par rapport au référentiel G, la portion
de trajectoire d'entrainement à l'instant t est une portion de cercle passant
par M*, point de la tige coïncidant avec M à cet instant.
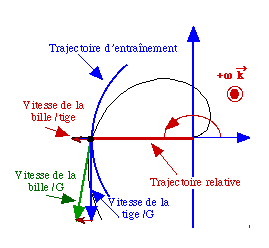
La trajectoire par rapport au référentiel
G est une portion de spirale.
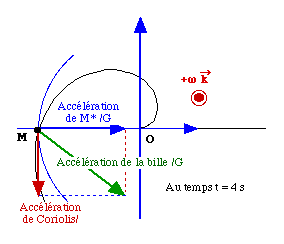
Au temps t = 4 secondes : q
= p rad et 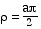
3°) Par rapport à R, l'accélération
du point M s'écrit :
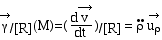
Dans ce cas, 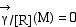 . .
La vitesse relative non nulle et le fait que R soit
en rotation, entrainent l'existence de l'accélération de Coriolis 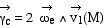 .
Ici, .
Ici,
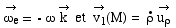 et et 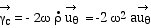
On a donc 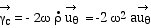 . .
Pour l'accélération d'entrainement,
le vecteur rotation étant de norme constante et les origines étant
confondues, l'expression générale se simplifie et il ne reste qu'à
calculer le double produit vectoriel 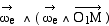 . .
L'expression de l'accélération par rapport
au référentiel G est alors :
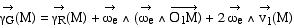
Soit dans la base cylindrique, nous retrouvons l'expression
bien connue :
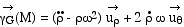 (M) (M)

|