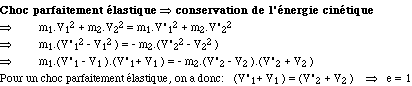Chocs durs (ou parfaitement élastiques).

Masse Gauche = 2 Masse Droite = 2 Coef de restitution = 1   Vitesse initiale Gauche Vitesse initiale Droite % énergie dissipée (1) 40 -40 0% (2) 40 -20 0% (3) 40 0 0%   Masse Gauche = 2 Masse Droite = 2 Coef de restitution = 1   Vitesse initiale Gauche Vitesse initiale Droite % énergie dissipée (1) 80 -80 0% (2) 80 -40 0% (3) 80 0 0%   Masse Gauche = 2 Masse Droite = 4 Coef de restitution = 1   Vitesse initiale Gauche Vitesse initiale Droite % énergie dissipée (1) 80 -80 0% (2) 80 -40 0% (3) 80 0 0%   Masse Gauche = 2 Masse Droite = 3 Coef de restitution = 1   Vitesse initiale Gauche Vitesse initiale Droite % énergie dissipée (1) 80 -80 0% (2) 80 -40 0% (3) 80 0 0%

La quantité de mouvement totale du système constitué par les 2 particules est égale à la somme des quantités de mouvement de chacune des particules Si le système constitué par les 2 particules est isolé, la quantité de mouvement totale de ce système est constante (avant et après le choc). Rappels: Par rapport au référentiel du laboratoire (supposé Galiléen), on note : V1 la vitesse de la particule 1 avant le choc V'1 la vitesse de la particule 1 après le choc V2 la vitesse de la particule 2 avant le choc V'2 la vitesse de la particule 2 après le choc Le coefficient de restitution est : 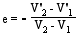La conservation de la quantité de mouvement donne : m1.V1 + m2.V2 = m1.V'1 + m2.V'2 m1.( V'1 - V1 ) = - m2.( V'2 - V2 ) ( 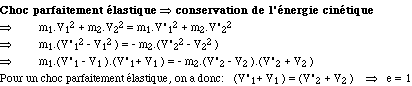dans le cas d'un choc mou, le coefficient de restitution vaut : e = 0 )