|
|
 |
|
|
|
Méthode de Bessel et de Silbermann
applicable aux lentilles convergentes
|
Etablissons
la relation qui existe entre la distance objet-image:  et la position de l'objet
En appliquant la relation de conjugaison: |
on en déduit: 
d'où 
soit: 
La fonction D = f (
p ) n'est pas définie pour p = - f ' et 
la courbe est asymptote à la droite
d'équation D = f ' - p
|
la dérivée
vaut: 
étudions le signe de cette dérivée en fonction de p. d'où la courbe représentative de D en fonction de p. Pour une lentille convergente la partie de la courbe en pointillés rouge n'a pas de signification physique puisque l'objet et son image seraient virtuels. Calculons les abscisses des points d'intersection p1 et p2 de la courbe D = f ( p ) avec la droite D = constante. |
Elles sont solution
de: 
les solutions sont donc:
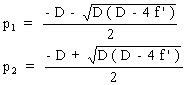
à condition que D (D - 4 f ' ) >=0 soit D >= 4 f '
Méthode
de Bessel
si D > 4 f ' on peut écrire:
|
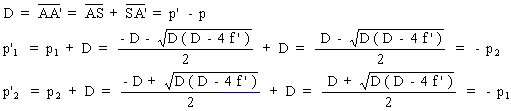
Etant
donné une lentille convergente de distance
focale
f ' et à condition que D > 4 f ' il existe deux positions S1 et S2 pour lesquelles la lentille convergente donne en
A' l'image nette d'un objet placé en A.
|
soit:
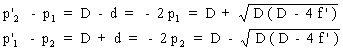
en multipliant membre à membre ces deux équations:
on en déduit:
La méthode de Bessel pour déterminer la distance focale f ' consiste donc à s'imposer une distance D entre un objet A et un écran E et à rechercher les deux positions de la lentille L qui donnent une image nette de A sur l'écran E. En mesurant les distances D et d on calcule la valeur de la distance focale f '. S'il n'est pas possible de trouver ces deux positions on augmente la valeur de la distance D qui sépare l'objet A de l'écran E.
Méthode de Silbermann
Cette méthode est un cas particulier de la méthode de Bessel.
|
Si D
= 4 f ' alors p = - 2 f ' et p' = 2 f '.
L'image et l'objet sont symétriques par rapport à S et le grandissement vaut -1: l'objet et son image sont situés dans les plans antiprincipaux. |
On déduira donc la valeur de la distance focale f ' de la lentille en diminuant la distance D qui sépare l'objet de son image jusqu'à ce que l'image soit identique à l'objet mais renversée; on divise alors la distance correspondante par 4 pour obtenir f '.
L'animation didacticielle suivante illustre la détermination d'une distance focale par la méthode de Bessel et Silbermann:
|
Méthode de Bessel et Silbermann |
|
|
|
