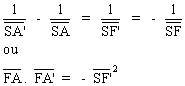
Ce qu'il faut retenir:
Principe

|
La
distance focaled'une lentille mince quelconque peut se déduire des
relations de conjugaison suivantes:
|
Méthode des points conjugués
applicable aux lentilles convergentes et divergentes
|
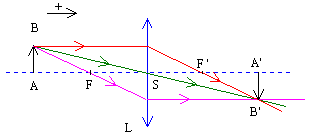
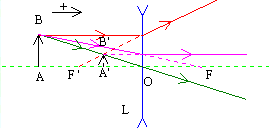
Une
lentille convergente L donne d'un objet A une image A'.
Posons La courbe:
L'ensemble du faisceau de segments de droite qui joignent les couples de points conjugués ( pn , p'n ) se coupent en un point de coordonnées f ' , f '. |
Méthode de Badal
applicable aux lentilles convergentes et divergentes
|
La lentille
l donne d'un point objet A une image à l'infini. La lentille
Lo de distance focale f 'o connue est placée derrière l à une distance
supérieure à sa distance focale f
'o ( Fo est entre l et Lo). Lo donne alors une image A'
de A dans le plan focal image E de Lo située en F'o.
On place alors la lentille L dont on cherche à déterminer la distance focale f ' dans le plan focal objet de Lo. Pour obtenir une image nette A' on doit déplacer l'écran E d'une distance D et l'on a:
|
Méthode de neutralisation
applicable aux lentilles convergentes et divergentes
|
Principe:
on accole à la lentille L de distance focale
inconnue une lentille l de vergence opposée de manière à ce que l'ensemble
se comporte comme une lame à faces parallèles.
On forme de l'objet O une image virtuelle O' et on déplace verticalement le système des deux lentilles ( L + l ) .On obtient un système de convergence nulle lorsque l'image reste fixe. |
Mesure des rayons de courbure
applicable aux lentilles convergentes et divergentes
|
On
peut également utiliser un sphéromètre pour mesurer les rayons de
courbures R1 et R2 des faces de la lentille et connaissant l'indice n
du verre de la lentille appliquer la relation:
|
Autocollimation
applicable aux lentilles convergentes
|
On déplace
l'ensemble ( miroir M + lentille L ) de manière à former l'image A'B' de
l'objet AB dans le plan de l'objet.
On mesure alors la distance entre l'objet et la lentille, distance qui correspond à la distance focale de la lentille L. |
Méthode de l'objet à l'infini
applicable aux lentilles convergentes
|
A l'aide d'une lentille auxiliaire L1 on forme une image d'un objet AB à l'infini, puis on interpose la lentille L, dont on cherche à mesurer la distance focale , entre cette lentille L1 et l'écran E. La distance qui sépare la lentille L à l'écran E mesurée lorsque l'image de l'objet AB est nette sur l'écran E correspond à la distance focale f de la lentille L. |
Méthode de Bessel
applicable aux lentilles convergentes
|
La méthode
de Bessel pour déterminer la distance focale f ' consiste donc à s'imposer
une distance D entre un objet A et un écran E et à rechercher les deux positions
de la lentille L qui donnent une image nette de A sur l'écran E. En mesurant
les distances D et d on calcule la valeur de la distance focale f '. S'il
n'est pas possible de trouver ces deux positions on augmente la valeur de
la distance D qui sépare l'objet A de l'écran E.
|
Méthode de Silberman
Cette méthode est un cas particulier de la méthode de Bessel.
|
On déduira donc la valeur de la distance focale f ' de la lentille en diminuant la distance D qui sépare l'objet de son image jusqu'à ce que l'image soit identique à l'objet mais renversée; on divise alors la distance correspondante par 4 pour obtenir f '. |