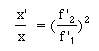|
|
 |
|
|
|
Association de deux Doublet.
|
Deux
lentilles
minces L1 et L2
de distances focale f '1 et f '2
séparées par: 
forment un doublet que l'on définit en général par son symbole, ensemble
de 3 nombres algébriques m, n et p, généralement entiers et tels que:
|
si l'on applique la formule de Gullstrand à cette association:
H'1 est en O1 et H2 est en O2 donc: 
et la convergence de l'association des deux lentilles
est donnée par:
où f ' est la distance
focale du doublet. Posons: 
et donc:
soit:
le foyer
image
F ' du doublet est le conjugué de F '1 dans L2:
d'où:
de même le foyer
objet
F est le conjugué de F2
dans L1: 
d'où:
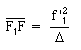
Tous les éléments cardinaux peuvent alors être mis en place.
Doublet symétrique.
|
Les doublets sont souvent symétriques et admettent le milieu C de O1O2 comme centre de symétrie. Les points nodaux objet N et image N' sont les conjugués de C à travers L1 et L2 respectivement. Les points antinodaux sont les foyers F1 et F '2. Le foyer objet F du doublet est le milieu du segment NF1. |
Doublet afocal.
|
Un doublet est afocal si l'image d'un objet à l'infini est également à l'infini. Les foyers F '1 et F2 sont confondus. Nous prendrons les foyers F1 et F '2 qui sont conjugués, comme origines pour fixer la position de l'objet AB et celle de son image A'B'.Un doublet est afocal si l'image d'un objet à l'infini est également à l'infini. Les foyers F '1 et F2 sont confondus. Nous prendrons les foyers F1 et F '2 qui sont conjugués, comme origines pour fixer la position de l'objet AB et celle de son image A'B'. |
Si l'on pose:
la
relation donnant le grandissement
axial s'écrit: 
soit:
|
|
|
