|
|
 |
|
|
|
Limite de résolution intrinsèque d'un instrument optiquement parfait.
|
Considérons un système centré optiquement parfait dont les pupilles d'entrée et de sortie Po et P'o limitent le faisceau utile dans les espaces objet et image. L'ouverture du faisceau utile conditionne seule le rayon de la tache d'Airy et les figures de diffraction sont celles que l'on obtiendrait en remplaçant le système par deux lentilles convergentes L et L' diaphragmées par Po et P'o et dont les distances focales seraient: CoF = CoA et C'oF' = C'oA'. |
Dans l'espace
image
les rayons des taches de diffraction sont vues du centre C'o de la pupille de sortie sous
le même angle 
( de même pour l'espace
objet et 
)
Dans l'espace
image la pupille de sortie limite le faisceau et 
est le rayon angulaire de la tache de
diffraction correspondant à un point objet à l'infini:
, de même
dans l'espace objet: 
si A' et
B' images des points A et B satisfont au critère de Rayleigh nous avons: 
et si le
système est aplanétique pour les points A et A': 
L'angle sous lequel la limite de résolution linéaire est vue de la pupille d'entrée ne dépend que du rayon de cette pupille et de la longueur d'onde:
si l'objet est à l'infini:
la limite angulaire de résolution de l'objet est
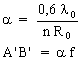
si l'objet
est dans le plan focal objet:
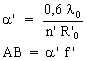
si l'objet
et l'image sont à distance finie
, sin u étant
inférieur ou égal à 1 et 
étant la longueur d'onde de la radiation dans le milieu
objet, on voit que:
Une radiation ne peut pas transmettre d'information sur des détails dont l'ordre de grandeur est inférieur à une demi- longueur d'onde.
|
|
|
