|
Systèmes centrés afocaux.
Un système centré sera dit afocal lorsque ses deux foyers sont rejetés à l'infini. Ainsi à tout incident parallèle à l'axe correspondra un émergent également parallèle à l'axe.
D'autre part le grandissement linéaire est constant et indépendant de la position et de la taille de l'objet.
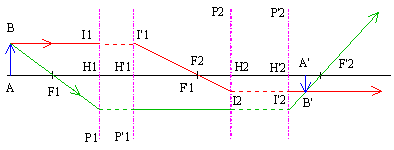
On a: ![]() soit:
soit:
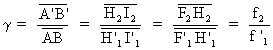
Puisque le grandissement linéaire est constant il en sera de même pour le grandissement angulaire.
On définira de plus le grandissement axial de deux points objet A et C, situés sur l'axe, dont A' et C' sont les deux points conjugués dans le système centré, par la relation:
![]()
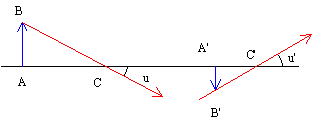 |
Dans les conditions
d'approximation de Gauss
on pourra écrire:
|
On en déduit le grandissement axial:
![]()
Le grandissement axial est une constante dans un système centré afocal.
On rencontrera de tels systèmes centrés afocaux dans les instruments d'optique destinés à faire l'observation d'objets éloignés et destinés à être utilisés par un observateur dont la vision est normale c'est à dire qu'il vise à l'infini sans accommoder. Ces instruments tels les lunettes et les télescopes comportent un objectif associé à un oculaire et pour rendre le système afocal il suffira de faire coïncider le foyer image de l'objectif avec le foyer objet de l'oculaire.