Thermodynamique chimique  Equilibres chimiques   Notion de variance  : 3) réactions hétérogènes et homogènes.

Variance d'un système : définition.

C'est le nombre de paramètres intensifs qu'il est nécessaire de connaître pour décrire quantitativement le système en équilibre.

Calcul de variance : Exemple 3. Reactions hétérogènes et homogènes

soit un système dans lequel les transformations chimiques suivantes peuvent se produire

I_{2  (gaz)}  + H_{2   (gaz)}   <=>      2 HI _(gaz)              réaction 1

I_{2  (solide)}   <=>   I_{2  (gaz)}                  réaction 2

Quelle est la variance du système à l'état d'équilibre lorsqu'on part d'un mélange équimolaire d'hydrogène et de diiode gazeux ?

Les paramètres intensifs qui permettent de décrire l'état du système à l'équilibre seront la température T (qui impose la valeur de K) , la pression totale p_t et les pressions partielles de I₂, H₂ et HI , p_I2 , p_H2 et p_HI. Soit 5 paramètres intensifs.

Ces paramètres ne sont pas indépendants les uns des autres puisqu'à l'équilibre les 2 relations suivantes seront vérifiées :

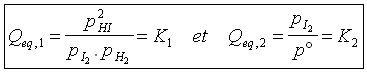
où p° représente la pression standard de référence , 1 bar .

En outre, nous aurons la relation p_t = p_HI + p_I2 + p_H2 . 

Il n'existe pas de relation supplémentaire due au fait que le mélange initial soit équimolaire car I_{2 (gaz)} est impliqué dans deux réactions. De ce fait il n'y a pas égalité entre les pressions partielles de I₂ et de H₂.

Ces 5 paramètres sont donc reliés entre eux par les 3 relations ci-dessus et par conséquent,  la variance du système à l'équilibre vaut

v = 5 - 3 = 2.

Le nombre de paramètres intensifs qu'il est nécessaire de connaître pour définir l'état du système est donc égal à deux, donc la variance vaut donc 2.

Formule "classique" .

La relation v = n + 2 - j où v est la variance, n le nombre de constituants indépendants (c.a.d. le nombre de composés chimiques concernés moins le nombre de relations entre eux) , le nombre 2 représente la pression totale p_t et la température et j le nombre de phases est souvent utilisée.

Dans l'exemple ci-dessus il y a 4 constituants dans le système (I2 gaz, I2 solide, H2 et HI ) et  deux transformations donc n = 4 - 2 = 2.

Le nombre de phases j = 2 (un solide et une phase gaz ) et la variance vaut donc v = 2 + 2 - 2 = 2.

Thermodynamique chimique  Equilibres chimiques   Notion de variance  : 3) réactions hétérogènes et homogènes.