|
C'est le nombre de paramètres intensifs qu'il est nécessaire de connaître pour décrire quantitativement le système en équilibre.
Les paramètres intensifs qui permettent de décrire l'état du système à l'équilibre seront la température T (qui impose la valeur de K) , la pression totale pt et les pressions partielles de A, B , C et D , pA, pB, pC et pD soient 6 paramètres.
Ces paramètres ne sont pas indépendants les uns des autres puisqu'à l'équilibre les relations suivantes seront vérifiées :
| relation 1 | relation 2 | relation 3 | relation 4 |
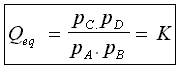
|
pA + pB + pC + pD = pt par définition des pressions partielles, |
pA = pB car les quantités de matière de A et B sont identiques si le mélange initial de A et B est équi molaire, |
pC = pD puisqu'il n'y a ni C ni D initialement. |
Ces 6 paramètres sont donc reliés entre eux par les 4 relations ci-dessus et par conséquent, et la variance du système vaut donc
v = 6 - 4 = 2.
Le nombre de paramètres intensifs qu'il est nécessaire de connaître pour définir l'état du système est donc égal à 2 , donc la variance vaut donc deux. Par exemple si la pression totale et la température sont imposées, alors la composition du système à l'équilibre est parfaitement définie et elle peut être calculée "a priori".
La relation v = n + 2 - j où v est la variance, n le nombre de constituants indépendants (c.a.d. le nombre de composés chimiques concernés moins le nombre de relations entre eux) , le nombre 2 représente la pression totale pt et la température et j le nombre de phases est souvent utilisée.
Dans l'exemple ci-dessus il y a 4 constituants dans le système (A, B, C et D ) , une seule réaction chimique mais aussi 2 autres relations entre les pressions partielles donc n = 4 - 3 = 1.
Le nombre de phases j = 1 (une seule phase gaz ) et la variance vaut donc v = 1 + 2 - 1 = 2.