exemple_2.htm

Chapitre 2
Approche formelle
de réactions simples

Réaction
d'ordre 1

Vous pouvez accéder à un exemple qui traite de la vérification de l'ordre 1 à partir

	du temps de demi-vie
	des vitesses
	des concentrations
	des concentrations... autre exemple.

Exemple de vérification de l'ordre 1 à partir du temps de demi-vie :

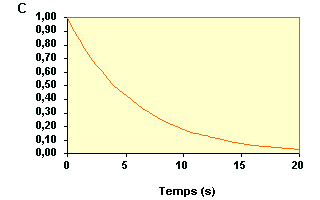	La variation de concentration du réactif A au cours du temps d'une réaction est représentée sur cette figure.
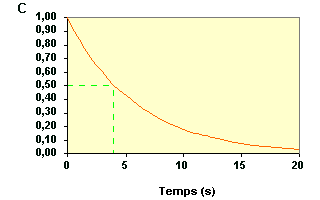	Déterminons graphiquement la date qui correspond à C= . On trouve : t₁ = 4 s. Donc la première période : t _1/2 = t₁ = 4 s
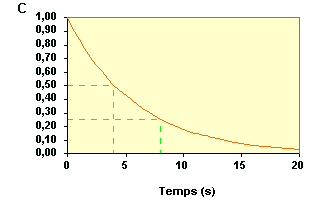	Déterminons la date qui correspond à C = 0,25. On trouve t₂ = 8,2 s. La deuxième période vaut donc : t₂ - t₁ = 8,2 - 4,0 = 4,2 s. On peut considérer que ces deux valeurs (4,0 et 4,2) sont sensiblement égales.
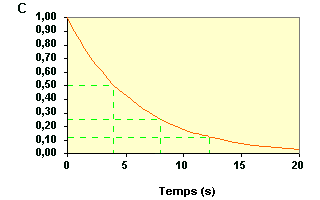	Cherchons à le confirmer en déterminant la date pour C = 0,125. On trouve : t₃ = 12,2 s . La troisième période vaut donc : t₃ - t₂ = 12,2 - 8,2 = 4,0 s. Ainsi, la valeur du temps de demi-vie déterminée pour différentes concentrations est sensiblement constante t₁ = 4,0 s ; t₂ - t₁ = 4,2 s et t₃ - t₂ = 4,0 s. Ceci permet de conclure que la réaction obéit à une loi d'ordre 1.
Remarque : Dans cet exemple, les temps de demi-vie sont très voisins. Il peut se faire que, compte tenu des erreurs expérimentales, on trouve des temps de demi-vie légèrement différents bien que la réaction soit du premier ordre.

Exemple de vérification de l'ordre 1 à partir des vitesses :

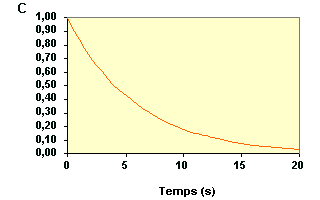
EXPB2B_1.gif (3746 octets)

A partir de cette courbe,
on peut déterminer graphiquement,
la vitesse de la réaction
pour différents instants.

On a trouvé les résultats suivants :
t (s)	2	4	6	8	10	12	16	20
v mol.L^-1.s^-1	0,121	0,086	0,061	0,044	0,031	0,022	0,011	0,006

Pour chaque point, on relève aussi la concentration, que l'on porte dans le même tableau.
t (s)	2	4	6	8	10	12	16	20
v mol.L^-1.s^-1	0,121	0,086	0,061	0,044	0,031	0,022	0,011	0,006
C mol.L^-1	0,071	0,051	0,036	0,026	0,018	0,013	0,007	0,003

On peut faire la vérification de la relation v = k. C_Asoit numériquement, soit graphiquement. De manière numérique, on calcule k pour les diverses valeurs de C_A et on s'assure que ces valeurs sont sensiblement constantes. On trouve les valeurs suivantes :
t (s)	2	4	6	8	10	12	16	20
k s^-1	1,70	1,69	1,69	1,69	1,72	1,69	1,57	2,00
On observe que pour les derniers points les valeurs s'écartent de celles obtenues pour les premiers points ; il est facile de voir que la précision sur ces deux derniers points est sensiblement moins grande.

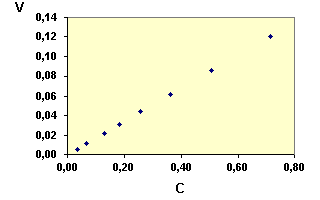	De manière graphique, on porte v en fonction de C_A et on constate que les points s'alignent bien sur une droite passant par l'origine
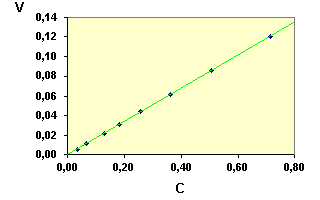	La droite passant par ces points a une pente égale au coefficient de vitesse. On trouve une pente égale à : 1,7 d'où k = 1,7 s^-1.
Remarque : Dans cet exemple, les points représentant la vitesse en fonction du temps sont parfaitement alignés. Il n'en sera pas toujours de même avec des valeurs expérimentales à cause de l'imprécision sur la détermination de la vitesse.

Exemple de vérification de l'ordre 1 à partir des concentrations :

La variation de concentration du réactif A au cours du temps d'une réaction est représentée sur la figure ci-dessous :
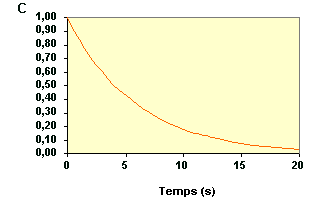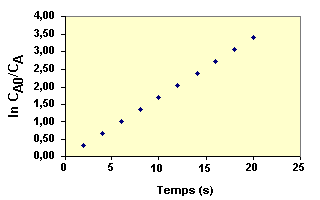
	La loi de vitesse sous sa forme intégrée s'écrit : En portant en fonction du temps, on doit trouver une droite de pente k.
	La figure suivante montre le graphe obtenu à partir de 10 points de la courbe précédente. On constate que les points sont bien alignés.

Autre exemple de vérification de l'ordre 1 à partir des concentrations :

La variation de concentration du réactif A au cours du temps d'une réaction est représentée sur la figure ci-dessous :
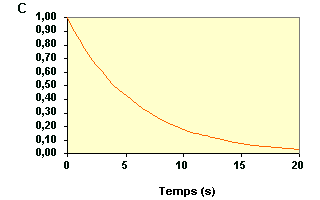	La loi de vitesse sous sa forme intégrée s'écrit :
On peut donc calculer la valeur de k pour chaque point par la relation : Avec 10 points de la courbe précédente, on trouve des valeurs constantes égales à 1,7 s^-1, ce qui montre que la réaction obéit à une loi d'ordre 1.
Remarque : Dans cet exemple, les points représentant en fonction du temps sont parfaitement alignés. Il n'en sera pas de même avec des valeurs expérimentales à cause de l'imprécision sur les mesures.

Chapitre 2
Approche formelle
de réactions simples

Réaction
d'ordre 1

Retour