 |
|
 |
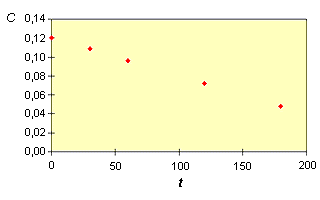
Les points
apparaissent bien comme alignés.
|
| Chapitre 2 Approche formelle de lois de vitesse d'ordre simple |
Réaction d'ordre 0 |
Exemple |
On a relevé les valeurs suivantes :
|
t (s) |
0 |
30 |
60 |
120 |
180 |
|
C (mol L-1) |
0,120 |
0,109 |
0,096 |
0,072 |
0,048 |
En portant sur un graphique C = f(t) on obtient :
 |
|
 |
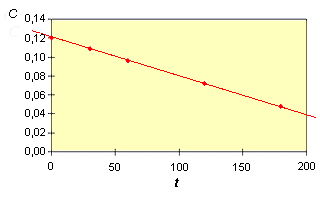
Les points
apparaissent bien comme alignés.
|
|
On peut aussi calculer les valeurs du coefficient de vitesse. On trouve : |
|||||
|
t (s) |
0 |
30 |
60 |
120 |
180 |
|
C (mol L-1) |
0,120 |
0,109 |
0,096 |
0,073 |
0,049 |
|
k x 104 |
3,67 |
4,00 |
3,92 |
3,94 |
|
Cliquez
ici si vous voulez des détails sur le calcul de k. On
note une différence entre la plus forte valeur et la plus grande de 0,33x10-4
soit environ 8% ce qui peut sembler un écart important. Cependant, on doit tenir
compte de l'incertitude sur les mesures.
Cliquez
ici si vous voulez des détails sur le calcul d'incertitude. Si
on considère que les concentrations sont connues avec 3 chiffres significatifs
et les mesures de temps à 1s près, un calcul d'incertitude montre que pour le
temps t = 30 s la précision sur k n'est que
de 20%. L'écart maximum observé (8%) est donc bien dans l'incertitude.
Nota : pour le temps t = 180, l'incertitude sur k
tombe à 3%.
Autres exemples :
Les réactions d'ordre zéro sont rares. Il ne peut
pas s'agir d'une réaction élémentaire, on est donc dans le cas d'une
dégénérescence d'ordre. Il s'agit toujours de réactions hétérogènes dont la
vitesse est limitée par la surface de contact entre phases.
La décomposition du pentoxyde de diazote N2O5 solide en NO2 et O2 est limitée par la sublimation du solide, celle-ci ne dépend pas de la concentration. La réaction est donc d'ordre 0 ; alors que si on opère directement en phase gazeuse elle est d'ordre 1.
La décomposition de PH3 (g) (phosphine) au contact d'un filament de tungstène chauffé se fait à vitesse constante. Cette vitesse dépend de la surface active du filament de tungstène. La réaction subit une catalyse hétérogène qui fixe la vitesse, donc impose un ordre égal à zéro.