Cette hypothèse se trouve d'ailleurs
corroborée
par le fait que la vitesse de ces réactions augmente
normalement avec la température selon un facteur en
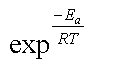
| Chapitre 4 Bases de la théorie... |
Théorie des processus pseudo monomoléculaires de Lindemann |
Théorie des processus pseudo monomoléculaires de Lindemann
La théorie des collisions ne permet pas de rendre compte des réactions qui obéissent à une loi du premier ordre.
En effet, selon la théorie des collisions, il faut qu'il y ait rencontre de deux molécules pour que la réaction puisse avoir lieu, ce qui conduit à une loi de vitesse du second ordre. Hormis le cas des réactions de désintégration radioactive et de quelques réactions de décomposition thermique qui sont véritablement monomoléculaires et pour lesquelles les molécules (ou du moins une fraction d'entre elles) possèdent une énergie interne suffisante pour se décomposer spontanément, on doit bien admettre que, pour un grand nombre de réactions qui suivent une loi du premier ordre, l'énergie d'activation doit être apportée par les chocs entre les molécules.
|
Cette hypothèse se trouve d'ailleurs
corroborée |
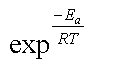 |
Comment dès lors expliquer cette contradiction
?
Cliquez
ici pour expliciter cette contradiction.
C'est Lindemann en 1922 qui a proposé un mécanisme
qui rend compte des observations pour les réactions en phase gazeuse.
Pour une décomposition d'une molécule A en B
et C :
A = B + C
L'activation se produirait lors d'un choc entre deux molécules A avec transfert d'énergie sur l'une d'entre elles qui se trouve alors dans un état d'énergie plus élevé :
|
A + A
|
a) étape d'activation bimoléculaire
(coefficient de vitesse k1 ) |
| Notation dans laquelle A* représente l'espèce A dans un état énergétiquement plus élevé. La molécule A* dans son état activé peut perdre son énergie dans une rencontre avec une autre molécule A (étape b) ou se transformer spontanément pour donner le produit de la réaction B (étape c). | |
|
A* + A
|
b) étape de désactivation |
|
A*
|
c) étape de transformation monomoléculaire |
La vitesse de la réaction peut être définie par la vitesse de formation du produit B.
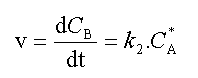 (1)
(1)
La concentration de A*
reste toujours très faible, on peut donc considérer qu'après une phase d'induction
sa concentration va rester quasiment stationnaire et écrire que sa vitesse de
transformation est presque nulle 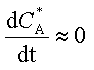 .
.
Remarque
:
Cette approximation qui consiste à considérer que la concentration d'un intermédiaire
reste faible et quasiment constante est appelée "Approximation de l'état quasi
stationnaire" ou "Hypothèse de l'état quasi stationnaire". Elle est largement
utilisée pour simplifier l'étude des système cinétique complexes lorsque qu'ils
font intervenir un intermédiaire de réaction qui ne s'accumule pas dans le milieu.
Elle sera reprise au chapitre 5 sur les "Réaction
composées" sous-chapitre "Réactions
séries" paragraphe sur l' "Etude
des cas limites".
Développons cette expression.
A* est formé par l'étape a) et consommé par les étapes b) et c).
D'où 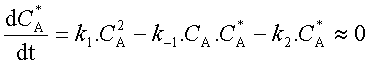
D'où l'on tire l'expression de la
concentration quasi stationnaire de A*
: 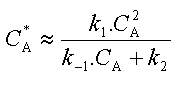
En portant cette expression dans la relation qui donne la vittesse de réaction (1) on obtient :
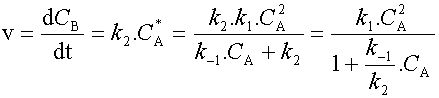 |
Cette loi de vitesse montre qu'en toute généralité
la réaction n'admet pas d'ordre.
Cependant, on peut considérer deux cas limites :
|
Si |
|
|
| ce qui se produit lorsque k-1
est beaucoup plus grand que k2 ou que CA
est très grand (soit en phase gazeuse pour de fortes pressions). Le processus
de désactivation bimoléculaire est plus rapide que la transformation monomoléculaire
de la molécule activée A* .
On peut négliger 1 devant 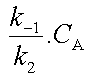
et la loi de vitesse se simplifie pour prendre la forme d'une loi du premier ordre 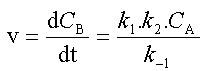 dont
le coefficient de vitesse observé est égal à dont
le coefficient de vitesse observé est égal à 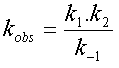 . . |
||
| Si | 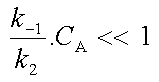 |
|
|
ce qui se produit lorsque c'est k2 qui est beaucoup plus grand que k-1 ou lorsque CA est très faible (soit en phase gazeuse pour de faibles pressions). C'est alors la transformation monomoléculaire de la molécule activée A* qui est plus rapide que sa désactivation bimoléculaire. On peut négliger |
||
En résumé,
selon les valeurs des coefficients de vitesse des différentes étapes et selon
la valeur de la concentration (ou de la pression de A) la réaction apparaitra
comme étant du premier ordre ou du second ordre, ou, dans les cas intermédiaires
n'obéira à aucun ordre.
Selon ce shéma, certaines réactions en phase gazeuse peuvent voir leur ordre changer avec la pression :
A haute pression Ordre 1
A basse pression Ordre 2
Pour des pressions intermédiares : pas d'ordre.