Les intervalles de R jouent un rôle fondamental dans l'étude des fonctions numériques (fonctions de R vers R), tant du point de vue global (ensemble de définition) que local (voisinage): ce sont les parties connexes, c'est à dire d'un seul tenant, de R.

La propriété de la borne supérieure (resp. inférieure) permet de classer les intervalles non vides de R en 9 types distincts suivant l'existence ou non d'un majorant, d'un minorant, d'un plus grand, d'un plus petit élément.

On montre ainsi qu'un intervalle non vide de R est d'un des types suivants :

intervalle borné

ouvert :	]a,b[ = {xR, a<x<b}
semi-ouvert :	[a,b[ = { xR, ax<b}
	]a,b] = { xR, a<xb}
fermé :	[a,b] = { xR, axb}

intervalle non borné

minoré, non majoré :

avec minimum [a,+[ = {xR, xa} sans minimum ]a,+[ = { xR, x>a}

majoré, non minoré :

avec maximum ]-,b] = { xR, xb} sans maximum ]-,b[ = { xR, x<b}

non minoré, non majoré :

]-,+[

Preuve : Par exemple, on peut montrer qu'un intervalle borné ayant un plus petit élément mais pas de plus grand élément est de la forme [a,b[ (Preuve).

Les intervalles ]a,b[ et [a,b], (b>a) peuvent être encore définis de la façon suivante :

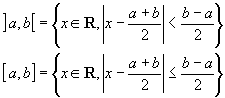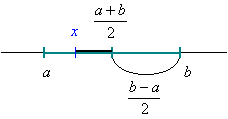Le réel est le centre de l'intervalle, est le rayon. Cette définition de l'intervalle ]a,b[, sera très souvent utilisée, en particulier, dans l'étude des suites et des fonctions.

Les propriétés locales font appel à la notion de voisinage d'un point.

Définitions. Soit aR, on dit que a est intérieur à un intervalle I s'il existe un intervalle ouvert contenant a et inclus dans I. On appelle voisinage de a toute partie de R qui contient un intervalle ouvert contenant a. On appelle voisinage de +(resp. -) toute partie de R qui contient un intervalle de la forme ]A,+[ avec AR, (resp.]-,B[ avec B R). On dit qu'une propriété est réalisée au voisinage d'un point s'il existe un voisinage du point dans lequel cette propriété est vérifiée .

Pratiquement on prendra pour voisinage de aR, les intervalles ouverts contenant a (fréquemment les intervalles ouverts centrés en a ) et pour voisinage de + (resp. -) les intervalles ]A,+[, (resp. ]-,B[).

Si V est un voisinage de a, on note V* =V-{a}, voisinage épointé de a .

Preuve : Ceci peut être démontré en utilisant une approximation décimale de (Preuve).

Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)