Théorème (Heine).   Soit f une fonction continue sur un intervalle fermé, borné 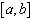;, la fonction f est uniformément continue sur .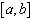

Preuve
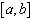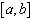Démonstration par l’absurde : on suppose que f, continue sur , n’est pas uniformément continue sur . Comme dans les théorèmes précédents sur des intervalles fermés bornés la démonstration s’appuie sur le théorème de Bolzano-Weierstrass (Preuve) .

Groupe MMM Maths UPI Université Pierre et Marie Curie (Paris 6)