Représentons pour différentes valeurs de a et b l'ensemble :
{ax + by -n 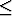 x
x 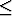 n -n
n -n 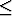 y
y 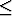 n} .
n} .
Observez sur les exemples les valeurs du tableau en cherchant quelle est la plus petite valeur positive du tableau et quel est le pgcd de a et b .
Le programme suivant permet de visualiser différentes valeurs de ax + by , où a et b sont deux entiers, et x et y sont des entiers compris entre - n et + n .
Testez les valeurs suivantes puis d'autres de votre choix. Les exemples qui vous sont proposés permettent de faire apparaître le pgcd de a et b pour une petite valeur de n.
Attention au temps de calcul, prenez de petites valeurs pour n !!!
- a = 26 b = 22 n = 8
- a = 135 b = 195 n = 5
- a = 71 b = 95 n = 5

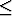 x
x 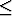 n -n
n -n 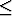 y
y 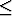 n} .
n} .