|
 |
Introduction
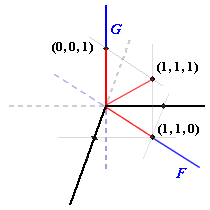 |
Dans R3, soit F le sous espace vectoriel engendré par |
Dans R3, soient les sous-espaces vectoriels F et G suivants :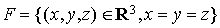 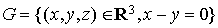 Alors F est contenu dans G, d'où 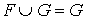 et et est un sous-espace vectoriel de R3. est un sous-espace vectoriel de R3.
|
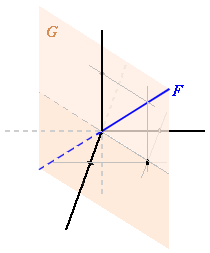 |
Donc dans un K-espace vectoriel E, la réunion  de deux sous-espaces vectoriels F et G peut être ou ne pas être un sous-espace vectoriel de E.
de deux sous-espaces vectoriels F et G peut être ou ne pas être un sous-espace vectoriel de E.