|
 |
 |
Structure de la réunion
|
Structure de la réunion de deux sous-espaces Soient E un K-espace vectoriel, F et G deux sous-espaces vectoriels de E. La réunion 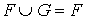 ou ou 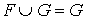 , , 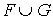 est un sous-espace vectoriel de E si et seulement F est contenu dans G ou G est contenu dans F. est un sous-espace vectoriel de E si et seulement F est contenu dans G ou G est contenu dans F.
|
 Preuve
Preuve
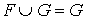 est bien un sous-espace vectoriel de E.
est bien un sous-espace vectoriel de E.
|
Méthodologie Si (P) désigne la propriété " c'est un raisonnement par contraposée.
|
|
Soit F et G tels que F ne soit pas contenu dans G, et G ne soit pas contenu dans F.
Puisque F n'est pas contenu dans G, il existe un élément de F, noté a, qui n'appartient pas à G. Comme F est contenu dans 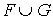 , a appartient aussi à
, a appartient aussi à 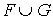 .
.
Et de même, puisque G n'est pas contenu dans F, il existe un élément de G, noté b, qui n'appartient pas à F. Comme G est contenu dans 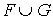 , b appartient aussi à
, b appartient aussi à 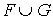 .
.
Alors l'élément 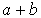 n'appartient ni à F ni à G :
n'appartient ni à F ni à G :
en effet s'il appartenait à F, l'élément 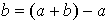 serait dans F puisque F est un sous-espace vectoriel, ce qui est en contradiction avec le choix de b; de même
serait dans F puisque F est un sous-espace vectoriel, ce qui est en contradiction avec le choix de b; de même 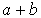 ne peut pas appartenir à G, sinon
ne peut pas appartenir à G, sinon 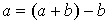 appartiendrait à G.
appartiendrait à G.
Donc puisque 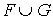 n'est pas stable pour l'addition,
n'est pas stable pour l'addition, 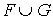 n'est pas un sous-espace vectoriel de E.
n'est pas un sous-espace vectoriel de E.