|
 |
 |
|
|
|
Exemple dans l'espace des fonctions
Soit l'espace vectoriel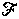 
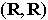des fonctions de R dans R.
Le sous-espace vectoriel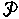 
des fonctions paires et le sous-espace vectoriel 
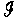des
fonctions impaires sont des sous-espaces supplémentaires.
=
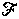
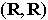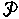
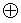
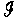
Preuve :
Si f est une fonction quelconque de ,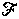
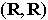il faut déterminer une fonction paire g et une fonction impaire h dont la somme soit égale à f.
Les fonctions g et h doivent vérifier :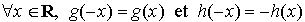 
.
Comme f doit vérifier pour tout x :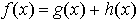 
(*),
elle vérifie aussi :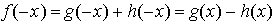 
.(**)
Des égalités (*) et (**) découlent les expressions de g et h suivantes :
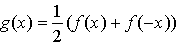et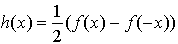 
Ceci démontre que les seules fonctions g et h avec g paire et h impaire
telles que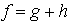 
sont celles qui précèdent.
Réciproquement il est facile de vérifier que pour toute fonction f, la fonction g
définie pour tout élément x de R par ""
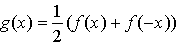est paire et que la fonction h définie pour tout élément x de R par
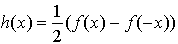"" est impaire et que .
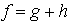Ceci démontre que toute fonction s'écrit d'une manière unique comme la somme d'une fonction paire et d'une fonction impaire.
|
|
|