|
 |
 |
Dans l'exemple 1 précédent, la somme 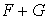 est
une somme directe, mais elle n'est pas l'espace vectoriel tout entier.
est
une somme directe, mais elle n'est pas l'espace vectoriel tout entier.
Dans l'exemple 2, F' et G' vérifient bien 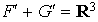 mais leur somme n'est pas directe.
mais leur somme n'est pas directe.
Les sous-espaces F et G ne sont pas des sous-espaces vectoriels supplémentaires, F' et G' non plus.
Soient les sous-espaces vectoriels F'' et G'' de R3 suivants :
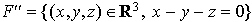 et
et 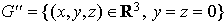
 Preuve :
Preuve :
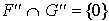 :
: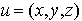 appartient à
l'intersection de F'' et de G'', alors les coordonnées de u vérifient :
appartient à
l'intersection de F'' et de G'', alors les coordonnées de u vérifient :
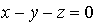 (car u appartient à F''),
et
(car u appartient à F''),
et 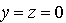 (car u appartient à G''),
(car u appartient à G''),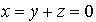 et
et 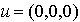 .
.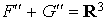 .
.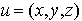 un élément quelconque de
R3 ; il faut déterminer des éléments
u1 de F'' et u2
de G'' dont la somme soit égale à u :
un élément quelconque de
R3 ; il faut déterminer des éléments
u1 de F'' et u2
de G'' dont la somme soit égale à u : 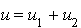 .
.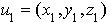 avec
avec 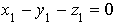 et l'élément u2
tel que
et l'élément u2
tel que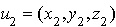 avec
avec 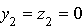 .
.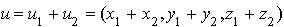 , les coordonnées de ces éléments doivent vérifier :
, les coordonnées de ces éléments doivent vérifier :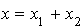 ,
, 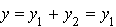 (puisque
(puisque 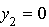 ),
), 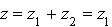 (puisque
(puisque 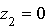 ),
),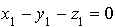 donc
donc
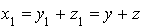 ,
,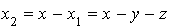 et donc
et donc 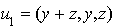 et
et 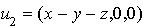 .
.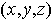 de R3 vérifie :
de R3 vérifie :
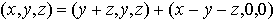 où
où 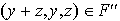 et
et 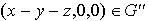 .
.
 Remarque :
Remarque :