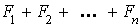Preuve de la propriété caractéristique
de la somme directe de plusieurs sous espaces

a) Supposons que la somme 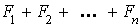est directe et montrons que

  

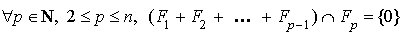
Soit p un entier compris entre 2 et n, et z un élément de  :

  
donc  
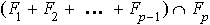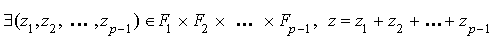
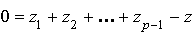
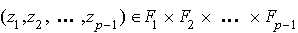avec et  ;
or 0 s'écrit d'une manière unique comme somme d'éléments de ,
donc .

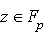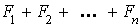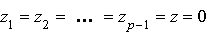b) Réciproquement, on veut démontrer que la propriété (P) :

"  "
implique la propriété (Q) :
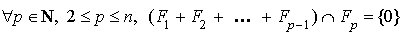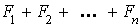"la somme est directe",
il est équivalent de démontrer que (nonQ) implique (nonP).

Supposons que la somme 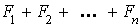n'est pas directe.
Il existe alors un élément z appartenant à 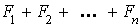admettant deux décompositions distinctes en somme d'éléments de ,
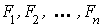c'est à dire :

  
et
  
tels que  
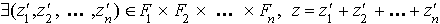
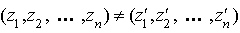
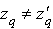Soit q le plus grand entier compris entre 1 et n tel que alors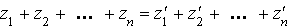
  implique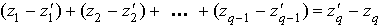
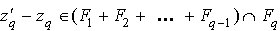donc et donc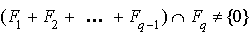
Ceci est bien la propriété (nonQ).


 Retour