|
 |
 |
Somme directe de plusieurs sous-espaces vectoriels
La notion de somme directe de deux sous-espaces vectoriels d'un K-espace vectoriel E se généralise au cas de plusieurs sous-espaces.
|
Définition de la somme directe de n sous-espaces vectoriels La somme de n sous-espaces vectoriels 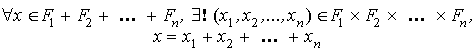 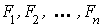 est notée : est notée :

|
La notation 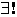 signifie : il existe un unique.
signifie : il existe un unique.
 Exemple
Exemple
Soit dans R4 les trois sous-espaces vectoriels F, G et H, engendrés
respectivement par (1,0,0,0), (0,1,0,0) et (0,0,1,0). Alors tout élément u de la
somme 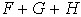 s'écrit sous la forme
s'écrit sous la forme
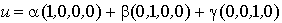 donc
donc 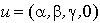 .
.
Si u s'écrivait aussi 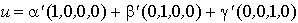 , alors
, alors 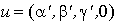 .
.
Mais dans R4 : 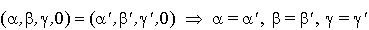
donc l'écriture d'un élément de 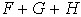 comme
somme d'éléments de F, G et H est unique :
comme
somme d'éléments de F, G et H est unique :
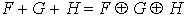
|
Propriété caractéristique La somme de n sous-espaces vectoriels |
Il est équivalent de dire d'après le théorème sur la somme directe de deux sous-espaces vectoriels :
|
La somme de n sous-espaces vectoriels 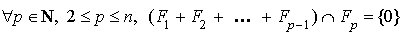 |
|
 Cliquez moi pour voir la preuve !
Cliquez moi pour voir la preuve !
Remarque :
Si 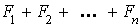 est une somme directe alors la propriété
suivante est vérifiée :
est une somme directe alors la propriété
suivante est vérifiée :
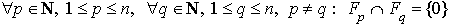
Mais cette condition (qui est nécessaire) pour que la somme soit directe n'est pas suffisante. En effet considérons le contre exemple suivant :
Contre exemple :
Dans l'espace vectoriel
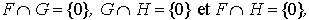 et pourtant la somme
et pourtant la somme
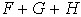 n'est pas directe.
n'est pas directe.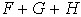 se décompose en somme d'éléments
de F, G et
H de la manière suivante :
se décompose en somme d'éléments
de F, G et
H de la manière suivante :
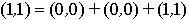
mais aussi de la manière suivante :
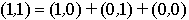
donc il n'y a pas unicité de l'écriture.
ATTENTION : Dans le cas de plusieurs sous-espaces vectoriels, le fait que les sous-espaces aient deux à deux une intersection réduite au vecteur nul n'est pas une condition suffisante pour que la somme soit directe.