|
|
 |
 |
 |
|
|
|
|
|
phrase 3
n 
N, 
p N, p 
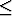n
phrase 4 p N, n
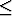N, p n
Rétablissons des parenthèses sous-entendues :
phrase 3 n N, ( p
N,
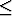p n )
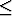La propriété " p N, p n" veut dire
que n est plus grand que tous les entiers. La phrase 3
signifie donc qu'il existe un entier n plus grand que tous les
autres. Ce qui est évidemment faux.
phrase 4 p N, ( n
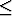N, p n )
La propriété " n
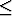N, p n" veut dire qu'étant donné p entier, on
peut trouver un entier n plus grand que p. La phrase 4
signifie donc que pour chaque entier p, on peut trouver un
entier plus grand, ce qui est vrai (par exemple p + 1 ou p + 15,
ou encore p lui-même ...).
