|
|
 |
|
|
|
 |
Considérons un conducteur sphérique de rayon R1
chargé d'une charge Q. Ce conducteur se trouve donc au potentiel
Les deux sphères se trouvent alors au même potentiel puisqu'elles
forment un conducteur d'un seul tenant. La charge Q se repartit en Q1
et Q2 de façon à ce que : |
Si s1 et s2
sont les densités superficielles de charge sur les sphéres :
et 
soit :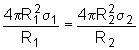 
Et puisque 
(théorème de Coulomb)
Puisque R1 / R2 > 1, le champ au voisinage du second conducteur est plus intense que le champ au voisinage du premier conducteur. C'est ce qu'on appelle le pouvoir des pointes : le champ est plus important dans les régions du conducteur de plus forte courbure.
 |
Extinction d'une bougie au voisinage d'une pointe chargée |
|
|
|
On relie ce conducteur à un second conducteur sphérique
de rayon R2 < R1 initialement neutre par un fil
conducteur supposé très long (influence négligeable).
soit 