Electrostatique Théorème de Gauss Cas d'une symétrie axiale

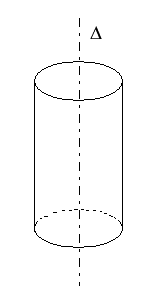
Une distribution de charges sources a une symétrie axiale si la densité de charges en un point M est uniquement fonction de la distance r à un axe d. Exemples :

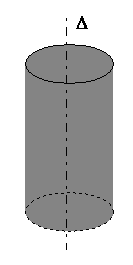
cylindre métallique chargé en surface	nuage de charges cylindrique de densité volumique r = cte	nuage de charges cylindrique de densité volumique r = f(r)

1. Par symétrie, le champ est radial (loin des bords de la source)

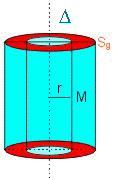
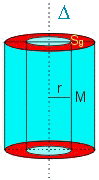
2.La surface de Gauss la plus adaptée est un cylindre axé sur  d et passant par le point d'étude M (celui-ci peut être intérieur ou extérieur à la source)

point d'étude extérieur à la source	point d'étude intérieur à la source

3.

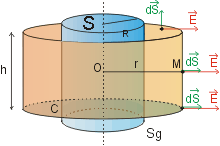Sur les sections droites S du cylindre Sg, les vecteurs et sont orthogonaux, le flux de à travers S est donc nul. Le flux de à travers la surface de Gauss fermée est reduit au flux à travers la surface latérale.

Sur la surface latérale et sont colinéaires donc le flux se reduit à :

E est le même en tout point de S_g et peut donc être sorti de l'intégrale :

or la surface latérale de la surface de Gauss est égale à  2prh

F = E . 2prh

Il ne reste plus qu'à évaluer la charge Q_i intérieure au volume délimité par S_gsuivant la distribution considérée. La théorème de Gauss permet alors de déterminer le champ E en écrivant :

E créé par un plan chargé uniformément

Electrostatique Théorème de Gauss Cas d'une symétrie axiale