Electrostatique Théorème de Gauss Cas d'une symétrie sphérique

Une distribution de charges sources a une symétrie sphérique si la densité de charges en un point M est uniquement fonction de la distance r à un centre O et non pas de la direction .

Exemples:

sphère métallique chargée en surface	nuage de charges sphérique de densité volumique   = constante	nuage de charges sphérique de densité volumique r = f(r)

1. par symétrie le champ est radial
2. La surface de Gauss la plus adaptée est une sphère centrée sur O et passant par le point d'étude M (celui-ci peut être intérieur ou extérieur à la source)

point d'étude extérieur à la source	point d'étude intérieur à la source

3.

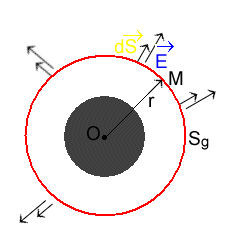le flux s'exprime simplement. En effet : et sont colinéaires. Donc le flux F se reduit à :

E est le même en tout point de S_g par symétrie et peut donc être sorti de l'intégrale

or l'aire totale de la surface de Gauss  S_g = 4pr² donc F = E.4pr²

Il ne reste plus qu'à évaluer la charge  intérieure au volume délimité par S_g suivant la distribution considérée. Le théorème de Gauss permet alors de déterminer l'amplitude du champ E en écrivant : 

Electrostatique Théorème de Gauss Cas d'une symétrie sphérique