|
|
![]() Principe
Principe
Cette représentation permet d'illustrer de manière simple les vibrations sinusoïdales de même fréquence, de comparer leurs phases et de les additionner.
Soit une vibration de forme générale s = a cos ( w t + F ) où F est un terme de phase global qui s'explicitera en fonction du type d'onde étudié.
|
Cette
vibration est représentée par la composante suivant l'axe:
à l'instant
t = 0 il fait un angle +
F avec
l'axe de vecteur unitaire |
Les angles sont orientés dans le sens
trigonométrique direct. L'extrémité P du vecteur décrit donc, à la vitesse angulaire
w, un cercle de centre O et de rayon a. Le vecteur ![]() est représenté à l'instant t = 0. Soit une vibration lumineuse
représentée en M de côte z par:
est représenté à l'instant t = 0. Soit une vibration lumineuse
représentée en M de côte z par:
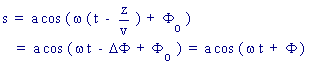
on lui associe le vecteur ![]() faisant, à l'instant t = 0, l'angle
faisant, à l'instant t = 0, l'angle ![]()
Au fur et à mesure que
l'onde se propage dans le sens Oz , la différence de phase évolue suivant ![]() et le vecteur
et le vecteur ![]() tourne
sur le cercle de rayon a. Deux points M et M' vibreront en phase lorsque
tourne
sur le cercle de rayon a. Deux points M et M' vibreront en phase lorsque ![]() et
et
![]() associés dans la représentation de Fresnel feront avec l'axe
associés dans la représentation de Fresnel feront avec l'axe ![]() le
même angle.
le
même angle.
La représentation d'une onde lumineuse par le vecteur de Fresnel et la différence de marche sont visualisées dans les animations suivantes:
![]() Addition de deux vibrations de même fréquence
Addition de deux vibrations de même fréquence
|
Pour
additionner deux vibrations de même fréquence en un point M de l'espace, on associera à
chacune des vibrations: - un vecteur - un vecteur La somme vectorielle |
On détermine ainsi la vibration résultante à partir d'une représentation vectorielle qui permet de déterminer l'amplitude A et la phase F sans faire de calcul. Dans le cas des interférences lumineuses, on considérera, afin de simplifier le calcul, qu'au point M arrivent deux vibrations de même fréquence et de même amplitude.
L'addition de deux vibrations: ![]() et
et ![]() donne:
donne:
![]() par le calcul
par le calcul
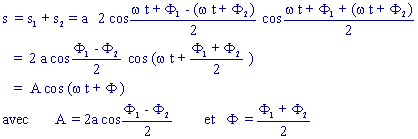
![]() par la représentation de
Fresnel:
par la représentation de
Fresnel:
|
Le
quadrilatère 0 P S Q étant un losange on a donc:
|
On a vu que l'intensité lumineuse est
proportionnelle au carré de l'amplitude soit pour la vibration s1
et la vibration s2 de même amplitude: ![]()
La vibration résultante s = s1 + s2 , d'amplitude A, aura pour intensité:
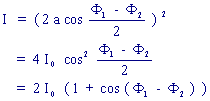
où ![]() représente le déphasage entre les vibrations s1 et s2 arrivant en
M.
représente le déphasage entre les vibrations s1 et s2 arrivant en
M.
|
Représentons
l'intensité lumineuse en fonction de L'intensité minimale est Imin = 0 et les interférences sont alors destructives. On peut remarquer que la valeur moyenne de I est égale à la somme des intensités des deux vibrations: I moyen = Is1 + Is2 |
![]()
![]()
varie de manière aléatoire au cours du temps et donc: I moyen = 2 I0 , c'est à dire l'intensité de deux fois l'une des vibrations.
L'addition de deux vibrations lumineuses de même amplitude est visualisée dans l'animation suivante: