|
|
|
|
(cas des lames à faces parallèles en lumière monochromatique)
Considérons une lame à faces parallèles d'indice n plongé dans un milieu d'indice n0 moins réfringent : n0 < n. Ici le milieu d'indice n0 est l'air. Un rayon incident R0 arrive sur la lame en un point I1 où il est réfléchi ( pour donner un rayon R1) et réfracté suivant I1J1.
|
Au point J1
ce rayon est partiellement réfléchi suivant J1I2 puis
partiellement réfracté pour donner un deuxième rayon R2 parallèle au
rayon R1. De même en J1, nous avons un rayon transmis T1 auquel on pourrait associer d'autres rayons T2...Tn. Un seul rayon incident R0 donne donc une série de rayons par réflexion R1....Rn parallèles entre eux et une série de rayons transmis parallèles entre eux et au rayon incident. |
L'amplitude - donc l'intensité - des rayons réfléchis et réfractés par la lame dépend du pouvoir réflecteur r de celle-ci.
Soit I0 l'intensité des rayons incidents,
Ir l'intensité des rayons après une réflexion et It l'intensité des rayons après une
réfraction. Le pouvoir réflecteur r est défini, en supposant que la lame n'absorbe pas
la lumière, par: ![]() .
.
L'intensité du rayon R1 vaut alors: I 1 = I 0 . r ,
![]()
![]()
Prenons par exemple: r = 0,04, pour une lame de verre d'indice n = 1,5 sous incidence quasi normale; alors
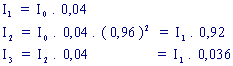
Nous ne considérerons que les deux premiers rayons réfléchis dans nos calculs puisque l'intensité des rayons suivants est négligeable par rapport à celle des deux premiers.
Le cheminement des rayons lumineux à travers une lame mince d'épaisseur constante est visualisée dans l'animation suivante:
| Lame mince à épaisseur constante. |
Le cheminement des rayons lumineux à travers une lame mince d'épaisseur constante est visualisée dans la vidéo suivante:
|
|
Lames minces
|