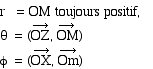Mécanique. Représentation de l'espace. 10

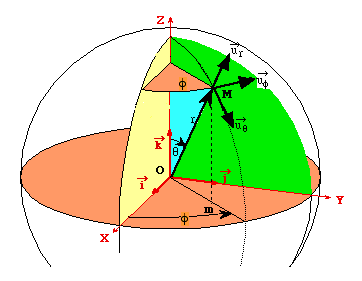
1.10. Coordonnées sphériques Repérage sphérique Vecteur élémentaire La base et les coordonnées (r,q, f) sont définies ci-dessous : Le point M est repéré par ses coordonnées sphériques : Dans la base sphérique , le vecteur position s'écrit .   La ligne coordonnée associée à r est la droite OM dont la direction varie avec M. La ligne coordonnée associée à q est le cercle de centre O, de rayon OM dans le plan (OM,OZ). La ligne coordonnée associée à f est le cercle de centre C, de rayon CM dans le plan (XOY). L'animation ci-dessous montre le repérage sphérique : la base et les coordonnées d'un point Le repérage sphérique L'animation ci-dessous montre l'ensemble du repérage sphérique : de la base, des coordonnées et de leurs accroissements élémentaires Vecteur élémentaire en coordonnées sphériques Les vecteurs de base, indiqués sur la figure, forment une base orthonormée directe et cette base, dépendante de M, est locale. Le vecteur position s'exprime dans la base sphérique : . Remarque: Il n'a pas de composante selon . La rotation du cercle de centre O, de rayon r engendre une sphère. Les relations entre coordonnées cartésiennes et coordonnées sphériques de M s'obtiennent à partir de considérations géométriques: x = r sin q cos f y = r sin q sin f z = r cos q

Mécanique. Représentation de l'espace. 10