Mécanique. Représentation de l'espace. 9

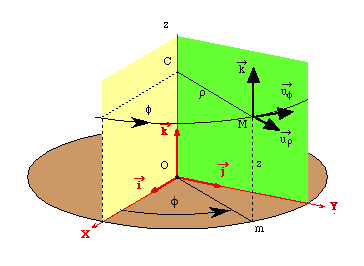
1.9. Coordonnées cylindriques Repérage cylindrique Vecteur élémentaire La base et les coordonnées (r, f, z) sont définies comme suit : Soit m la projection de M sur le plan (xOy). r = Om = CM toujours > 0 z = OC = mM Si on fixe f et z en faisant varier r, M décrit la droite CM : La ligne coordonnée associée à r est une droite. La ligne coordonnée associée à f est un cercle de centre C, de rayon CM, tracé dans un plan parallèle à (xOy). Enfin la ligne coordonnée associée à z est une droite mM toujours parallèle à Oz.   L'animation ci-dessous montre l'ensemble du repérage cylindrique : la base, et les coordonnées Le repérage cylindrique L'animation ci-dessous montre l'ensemble du repérage cylindrique : de la base, des coordonnées et de leurs accroissements élémentaires Vecteur élémentaire en coordonnées cylindriques Les vecteurs de base sont constamment tangents aux lignes coordonnées. Ils sont orientés dans le sens croissant de la coordonnée correspondante : dans le sens de r croissant , dans le sens de f croissant, dans le sens de z croissant. Ils forment une base orthonormée directe et la direction de dépend du point M. C'est pourquoi la base des coordonnées polaires cylindriques est dite base locale.    Le vecteur position s'exprime alors dans la base cylindrique : Remarque: Il n'y a pas de composantes selon. La rotation du plan autour de Oz engendre un cylindre. Les relations entre coordonnées cartésiennes et polaires cylindriques sont données par : x = r cos f y = r sin f z = z

Mécanique. Représentation de l'espace. 9