Espace_Physique

Mécanique. Représentation de l'espace 3

1.3. Structure d'espace vectoriel

Les mathématiciens préfèrent penser que c'est parce que l'ensemble des vecteurs de l'espace a cette structure qu'un de ses éléments est appelé vecteur ; c'est aussi ce qui le rend plus intéressant que les bipoints.

R est l'ensemble des nombres réels , E est un ensemble muni de deux lois:

• l'addition (opération interne):

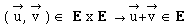
• la multiplication (opération externe):

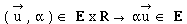
Le vecteur 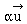est dit colinéaire à .

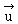Ces deux opérations - interne et externe - font de E un R -ESPACE VECTORIEL parce que :

• l'opération interne donne à E une structure de GROUPE COMMUTATIF :

• Addition

associativité :

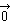est l'élément neutre de l'addition :

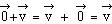
tout vecteur 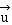admet un symétrique (ou opposé) :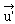

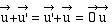
commutativité :

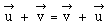
• les deux opérations vérifient les propriétés suivantes

• Addition et Multiplication par un scalaire

1 est l'élément neutre de la multiplication :

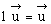
associativité :

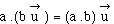
distributivité par rapport à l'addition des vecteurs :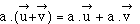

distributivité par rapport à l'addition des scalaires :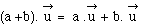

Mécanique. Représentation de l'espace 3