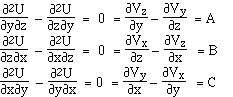Mécanique. Champs de vecteurs - Potentiel.5

3.5.Condition pour qu'un champ dérive d'un potentiel. Rotationnel.   Il est équivalent de dire qu'un champ dérive d'un potentiel ou que ce champ est un gradient. La condition pour qu'un champ dérive d'un potentiel est donc aussi bien la condition pour qu'un vecteur champ soit un vecteur gradient. • En coordonnées cartésiennes,  s'écrit Sous réserve que la fonction potentiel soit deux fois dérivable, ses dérivées croisées sont égales (Conditions de Schwartz ): Par définition, le vecteur dont les composantes sont A,B,C est le rotationnel de On le note La condition pour que dérive d'un potentiel scalaire U est   Remarque : Pour retrouver sans trop de mal les composantes du rotationnel, et celles du gradient, on introduit parfois un vecteurappelé nabla, opérateur de dérivation symbolique, dont les "composantes" sont: . Le gradient est alors l'application de nabla à la fonction U :                          Le rotationnel s'obtient par le produit vectoriel                       en coordonnées cartésiennes, on peut facilement retrouver les composantes à l'aide du "déterminant symbolique".

Mécanique. Champs de vecteurs - Potentiel.5