Mécanique - Chapitre A - 1

A.1. Description du mouvement d'un point matériel Notion de référentiel Description des mouvements dans l'espace-temps d'un observateur Equation horaire Variations élémentaires du vecteur position      Coordonnées Cartésiennes      Coordonnées Cylindriques       Coordonnées Sphériques      Base locale du mouvement  A.1.1. Notion de référentiel  La description du mouvement d'un point matériel exige de connaître sa position dans l'espace à tout instant. Pour cela, en plus du repérage de l'espace physique, il faut définir un phénomène physique (deux passages consécutifs du Soleil au zénith, l'écoulement d'un fluide contenu dans un récipient percé...) appelé chronologie qui permette , à l'aide d'un dispositif de mesure approprié ( réalisant notamment l'entretien du mouvement, le choix de l'unité...) de donner l'information accessible à l'utilisateur : 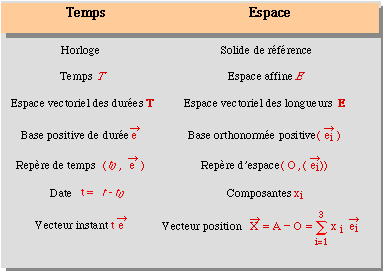ce dispositif est appelé horloge    La manière de formaliser le repérage du temps est analogue à celle du repérage de l' espace.       Analogie des notations de l'axiomatique du temps et de l'espace  L'ensemble repère-horloge constitue un référentiel La description du mouvement d'un mobile se fait donc dans un référentiel qui doit être défini sans ambiguité et toujours clairement énoncé..    En résumé, tout observateur est muni d'un temps T associé à une horloge et d'un espace affine E (ou vectoriel E) euclidien orienté à trois dimensions.    Faire l'exercice suivant Identification du référentiel    A.1.2. Description des mouvements dans l'espace-temps d'un observateur  Supposons qu'il existe des corps suffisamment petits appelés particules pour qu'ils ne coïncident qu'avec un seul point de l'espace.   A tout instant t, il existe un point M(t) de E avec lequel coïncide la particule à l'instant t.   Le point M(t) est la position de la particule p dans l'espace E à l'instant t.    Dans l'espace physique à trois dimensions, il faut trois données pour définir la position d'un point M: ce sont les coordonnées. Par exemple, r, f et q constituent les coordonnées sphériques.   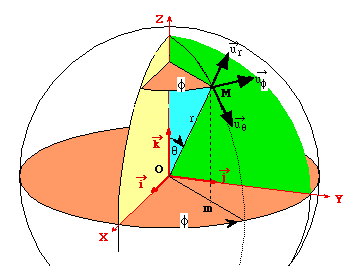La trajectoire de la particule p dans E est l'ensemble de ses positions {M(t)} lorsque t décrit l'intervalle de définition. Elle est définie par rapport à un référentiel.  Les expressions des coordonnées de M s'appellent les équations paramétriques du mouvement. En coordonnées cartésiennes, les équations paramétriques de M sont : x(t), y(t), z(t) ; en coordonnées cylindriques, elles sont r (t), f(t), z(t). Remarque:  En coordonnées cartésiennes, composantes et coordonnées ont la même expression; dans les autres systèmes de repérage, certaines composantes peuvent être nulles. Par exemple, en coordonnées sphériques; les composantes sur  et sont nulles.     A.1.3. 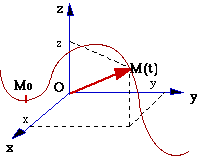Equation horaire    La trajectoire étant connue, pour repérer le mobile sur cette courbe, on peut choisir une origine M0 et un sens de parcours (sens positif) : on mesure alors la longueur de l'arc . On appelle abscisse curviligne s de M un nombre algébrique ayant pour valeur absolue la mesure de la longueur de l'arc et pour signe celui associé au sens positif choisi. Si la courbe est fermée (mouvement circulaire par exemple) à une même position de M peut correspondre une infinité d'abscisses curvilignes.     La fonction s(t) s'appelle l' équation horaire du mouvement sur la trajectoire.  L'équation de la trajectoire et celle de de l'équation horaire définissent entièrement la position de M à chaque instant, une fois donnée l'origine M0; ces équations sont équivalentes à l'équation du mouvement . Par contre, l'équation horaire seule (ou celle de la trajectoire) ne suffit pas à définir la position de M : deux mobiles peuvent se déplacer sur une même trajectoire avec des équations horaires différentes ou avoir des équations horaires identiques sur des trajectoires différentes.    A.1.4. 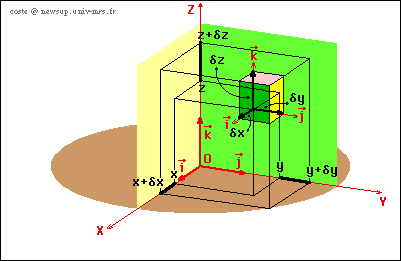Variations élémentaires du vecteur position   A.1.4.a) Coordonnées Cartésiennes  Le vecteur , variation du vecteur position s'exprime dans la base : où dx (respectivement dy, dz) correspondent aux variations de la position lorsque x (respectivement y, z) varie seul.   La simulation suivante montre la construction des composantes du point, les vecteurs de base, la variation de chaque coordonnée et la construction de l'élément de volume. 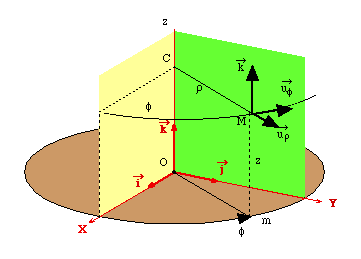Coordonnées cartésiennes Faire les exercices : Coordonnées cartésiennes Courbe engendrée par variation d'une coordonnée (en cartésien) Déplacement dû à la variation d'une coordonnée (en cartésien) Surface et volume élémentaire (en cartésien)    A.1.4.b) Coordonnées Cylindriques  Le vecteur , variation du vecteur position s'exprime dans la base : où dr (respectivement rdf, dz) correspondent aux variations de la position lorsque r (respectivement f, z ) varie seul.     La simulation suivante montre la construction des composantes du point, les vecteurs de base, la variation de chaque coordonnée et la construction de l'élément de volume. Coordonnées cylindriques Faire les exercices : Coordonnées cylindriques Champ de vecteurs unitaires (en cylindrique) Déplacement dû à la variation d'une coordonnée (en cylindrique) Surface et volume élémentaire (en cylindrique) Faire l'exercice suivant: Trajectoire elliptique    A.1.4.c) Coordonnées Sphériques  Dans la base sphérique , le vecteur position s'écrit Le vecteur , variation du vecteur position s'exprime dans la base , où dr (respectivement rdq, rsinq df) correspondent aux variations de la position lorsque r (respectivement q ,f ) varie seul. La simulation suivante montre la construction des composantes du point, les vecteurs de base, la variation de chaque coordonnée et la construction de l'élément de volume. 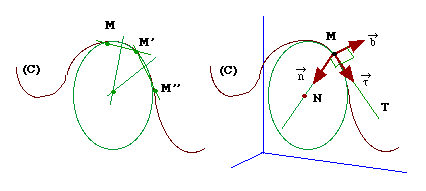Coordonnées sphériques Faire les exercices : Coordonnées sphériques Courbe engendrée par variation d'une coordonnée (en sphérique) Déplacement dû à la variation d'une coordonnée (en sphérique) Surface et volume élémentaire (en sphérique)    A.1.4.d) Base locale du mouvement   Soit un mobile M sur une trajectoire (C), courbe, orientée, non "pathologique", qu'il décrit dans le sens positif. Considérons trois positions successives très voisines M, M' et M" correspondant à des instants t, t' et t" tels que t'= t + Dt, t'' = t'+ Dt  Bien que la courbe (C) ne soit en général pas plane (on parle alors de courbe gauche), les trois points considérés définissent un plan P et un seul. De même par ces trois points passe un cercle situé dans P et dont le centre est déterminé par l'intersection des médiatrices des cordes MM' et M'M". Ce cercle est circonscrit à MM'M".  Quand D t tend vers zéro : - les axes définis par et tendent vers la tangente orientée MT. - le plan P tend vers un plan dit plan osculateur à (C) en M. - le cercle tend vers le cercle osculateur dont le rayon est le rayon de courbure R de (C) en M; son centre N est le centre de courbure. - MN est orthogonale à MT . MN est la normale principale à (C) en M et MT est la tangente au cercle en M. L'inverse K=1/R du rayon de courbure est la courbure. Le vecteur unitaire porté par la tangente orientée MT est . Le vecteur unitaire porté par la normale principale MN est . Le plan normal est le plan orthogonal à en M ; il contient évidemment la normale principale MN. On associe à et le vecteur unitaire, perpendiculaire en M au plan osculateur et tel que le trièdre soit direct; il est appelé parfois vecteur unitaire porté par la binormale.. Ces trois vecteurs constituent la base de Frenet. C'est une base orthonormée locale qui suit le mobile étudié, et donc dépend du temps.   Faire les exercices : Base intrinsèque en fonction du temps Base intrinsèque dans le plan Repérage sur une courbe Equation vectorielle d'un mouvement

Mécanique - Chapitre A - 1