Mécanique - Chapitre A - 2

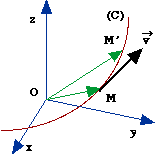
A.2. Vitesse du mobile par rapport à un référentiel  Définition Dérivée spatiale Unité    A.2.1- Définition.  Soit un mobile sur une trajectoire (C): à l'instant t, il est en M; à l'instant t'= t +Dt, il est en M'.  Par définition on appelle vecteur vitesse instantanée du mobile par rapport au référentiel [R]:             Par définition, cette limite est la dérivée du rayon vecteur par rapport au temps, elle se note : Il résulte de la définition que est un vecteur tangent en M à la trajectoire. Compte tenu de la définition de la vitesse et en introduisant l'abscisse curviligne, on peut écrire puisque s dépend de t : Mais par définition : Quand Ds tend vers 0, la norme de ce vecteur tend vers 1. ( est la longueur de la corde MM' et est la longueur de l'arc ; lorsque s' tend vers s, M' tend vers M, la corde tend vers l' arc ). Sa direction est celle de la tangente orientée MT , donc : De la définition de la vitesse, on déduit : en posant La dérivée par rapport à une variable scalaire t d'une fonction vectorielle se calcule en exprimant cette fonction vectorielle sur une base.   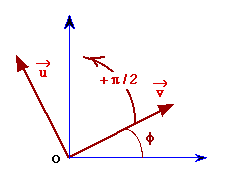Dérivée par rapport à f d'un vecteur: Soit un vecteur faisant l'angle variable f avec une direction fixe. La dérivée par rapport à f du vecteur unitaire est un vecteur unitaire déduite de par rotation dedans le sens des f croissants.      A.2.2 Unité  Du point de vue dimension ,une vitesse est le rapport d'une longueur à un temps: [v] = LT-1 Dans le système SI, une vitesse se mesure en mètre par seconde (m/s ou m.s -1). Résultat général Les expressions du vecteur vitesse s'obtiennent aisément à partir des expressions des variations élémentaires du vecteur position dans les divers systèmes de coordonnées

Mécanique - Chapitre A - 2