|
|
Mécanique - Chapitre A - 5 |
 |
|
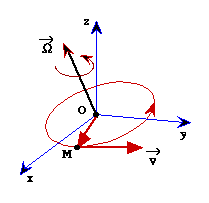
Soit une trajectoire circulaire de centre O dont le plan n'est pas fixe au cours du temps. A tout mobile M, animé sur cette trajectoire
d'une vitesse
où le trièdre
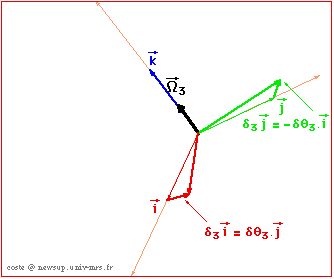
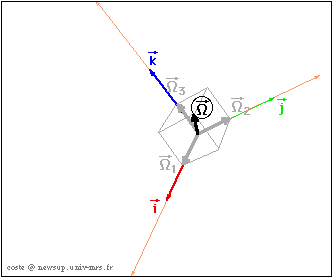
La simulation suivante montre les rotations élémentaires autour de chacun des trois axes de coordonnées
Compte tenu de la symétrie de ce mouvement, il est commode d'utiliser les coordonnées polaires planes. • La vitesse est donnée à partir de l' expression
sachant que r = R = cte et que • Le vecteur vitesse instantanée de rotation
est tel que: Soit: • L'accélération est donnée par l'expression
sachant que r = R = cte:
Pour ce mouvement, la base de Frenet est liée à la base locale :
L' accélération tangentielle est :
L' accélération normale :
L'accélération normale est centripète (dirigée vers le centre du cercle), elle est liée à la courbure de la trajectoire.
•• Le mouvement est circulaire uniforme: La vitesse horaire est constante, le vecteur vitesse
est L'accélération tangentielle est nulle et l'accélération normale de norme constante. Le temps mis pour faire un tour s'appelle la période T, elle se mesure en seconde (s). L'inverse de la période s'appelle la fréquence n; elle mesure le nombre de tours effectués par unité
de temps. Elle s'exprime en Hertz (Hz) :
W est le rapport de la mesure d'un angle et d'un temps. W s'exprime en radian par seconde (rad/s ou rad.s-1)
|
A.5. Vecteur vitesse
instantanée de rotation
A.5.1.
Rotation du vecteur position
dans un référentiel 
, on peut associer
un vecteur vitesse instantanée
de rotation 
défini par la relation suivante :
est direct.
changent à
chaque instant, il faut alors tenir compte du cas général des trois
rotations par rapport aux axes de référence.
. Sa norme 
est appelée
vitesse angulaire
,la vitesse horaire est donc v = RW (norme du vecteur vitesse);
par suite, la vitesse angulaire est constante ainsi que le vecteur vitesse instantanée
de rotation 
|
|
Mécanique - Chapitre A - 5 |
|