Mécanique - Chapitre B - 2

B.2. Composition des mouvements pour un point Composition des distances Déplacements d'un point par rapport à deux référentiels. Point coïncidant Passage d'un référentiel à l'autre   La cinématique des changements d'espace-temps (ou des changements de référentiels) a pour objet de relier les grandeurs de position, vitesse et accélération mesurées dans deux référentiels et par exemple, de déduire de la trajectoire d'un mobile dans un référentiel celle qu'il suit dans un autre.    Nous considérons ici deux observateurs dont les espaces-temps (E,T) et (E1T1) sont donnés. Le but est de déterminer les relations entre ces deux espaces-temps.  On admet que les deux observateurs ont la notion de simultanéité d'un instant t de T et t1 de T1. Ce principe de simultanéité suppose que la transmission de signaux entre les deux observateurs est instantanée, donc suppose la possibilité d'une vitesse infinie. Cette hypothèse n'est pas maintenue en Théorie de la Relativité Restreinte. On considère en cinématique classique que les horloges sont synchronisées dans tous les référentiels, donc la mesure du temps est un invariant. De même une longueur ou "distance instantanée" est invariante par changement de référentiel : si M et M' sont deux point matériels séparés de la distance d dans le référentiel [Ra], la distance instantanée d est invariante dans un autre repère [R], au même instant.   Remarque importante: Dans tout calcul de vitesse (ce qui se traduit par " dans toute dérivation vectorielle"), il est impératif de distinguer soigneusement les points (ou vecteurs) des divers espaces même s'ils coïncident à l'instant t.    B.2.1. 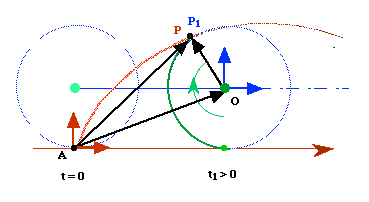Position d'un point par rapport à deux référentiels [Ra] et [R] On considère le mouvement d'une particule p dans [R]. On lui associe le point P1(t) : position de p dans [R] . Le mouvement de p dans [R] se nomme le mouvement relatif. Le mouvement de [R] /[Ra] est le mouvement d'entraînement La simulation suivante montre trois points fixes sur une roue, situés sur des rayons de tailles différentes. On associe à cette roue un référentiel [R] lié au centre de la roue et en translation par rapport au référentiel du laboratoire.  Les rayons passant par ces points de la roue tournent par rappor à [R]. La simulation montre leurs trajectoires par rapport au référentiel du laboratoire. 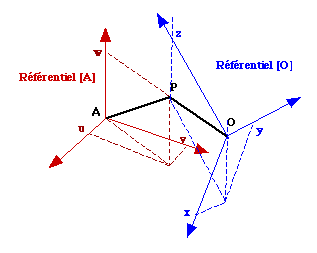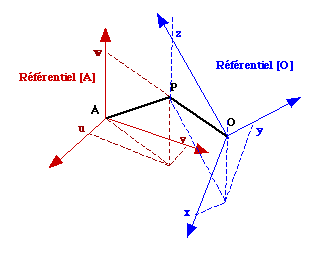Mouvement d'un point sur une roue Le mouvement composé de p dans [Ra] associe à l'instant t, le mouvement de p dans [R] et le mouvement de [R] /[Ra]. Soient les référentiels Soient u(t), v(t), w(t) les coordonnées de P(t) dans le référentiel [Ra] : Dans le référentiel centré en O(t) : : Dans [Ra], on peut écrire la composition des distances qui additionne les vecteurs position de p par rapport à [Ra] et position de p par rapport à [R]    B.2.2 Déplacements d'un point par rapport à deux référentiels. 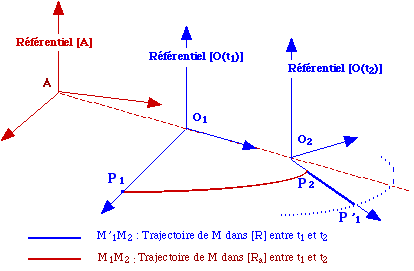On considère le référentiel [Ra] et dans ce référentiel, les positions du référentiel [R] à deux instants différents t1 et t2. Pour permettre une visualisation simple, le référentiel mobile subit une translation uniforme dans la direction Ov et simultanément, une rotation uniforme autour de Oz. Le point P a subi une translation sur Ox dans [R]. La figure montre que les deux trajectoires dans les deux référentiels sont complètement différentes. En se plaçant dans le référentiel [Ra], on a aux deux instants t1 et t2 où le point P occupe les positions P1 et P2: Soit P'1 le point, lié au référentiel [R], qui coïncide avec le point P1 à l'instant t1. Le déplacement du point P peut s'écrire dans [Ra]: . Le terme de gauche de l'égalité traduit le déplacement dans [Ra] du point P . Le premier terme de droite traduit le déplacement dans [Ra] du point P' (point du référentiel [R] coïncidant avec P à l'instant t1). . Le second terme de droite est le déplacement de P dans le référentiel mobile [R] . Le déplacement de P dans [Ra] peut donc être relié au déplacement de P dans [R] et à celui du référentiel [R] par l'intermédiaire du point coïncidant. Les vitesses seront les limites des rapports des déplacements à la quantité t2- t1 pour t2Æt1. On aura donc une vitesse "absolue" égale à la somme de la vitesse d'entrainement (celle du point coïncidant) et de la vitesse "relative". Trajectoire et vitesse n'ont de signification que par rapport à un même référentiel. Trajectoire et vitesse n'ont de signification que par rapport à un même référentiel. Remarque importante: Il convient de bien distinguer deux notions : - la notion de vecteur cinématique (respectivement vecteurs position, vitesse ou accélération) par rapport à un référentiel, - la notion de vecteur (quel qu'il soit) exprimé dans un repère ; dans ce dernier cas, il ne s'agit que d'exprimer les composantes d'un vecteur dans une base, même si ce vecteur représente une grandeur dynamique par rapport à un autre référentiel. Notations : Pour distinguer les vitesses et les accélérations par rapport à chaque référentiel, nous noterons généralement : Le plus souvent, pour des raisons pratiques, il sera fait la distinction entre un repère fixe et un autre mobile. Mais d'un point de vue cinématique cela n'a aucune importance. L'observateur situé dans un référentiel peut le considérer comme fixe et dire que l'autre est mobile.  B.2.3. Passage d'un référentiel à l'autre Si nous nous plaçons dans [Ra] la vitesse de P est : Si nous nous plaçons dans [R] la vitesse de P est : Pour étudier le passage de [Ra] à [R] on utilise la relation de composition des distances, valable à tout instant : Pour calculer les vitesses de ces vecteurs, un observateur de [Ra] dérivera cette expression dans son référentiel : est la vitesse de O dans [Ra] Si l'on connait, dans [Ra], la vitesse de P et celle de O, on connait évidemment aussi la dérivée de . Ce qui nous intéresse est : en relation avec . Il s'agit en fait d'exprimer la relation entre les dérivées par rapport au temps d'un même vecteur,  calculées dans deux référentiels différents.

Mécanique - Chapitre B - 2