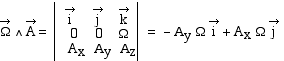Mécanique - Chapitre B - 3

B.3. Dérivée d'un vecteur dans un changement de référentiel Référentiels en translation l'un par rapport à l'autre [R] animé d'une rotation d'axe Az par rapport à [Ra] [R] en rotation d'axe D par rapport à [Ra] Considérons un vecteur qui s'écrit: - dans [Ra]: - dans [R] : Nous allons calculer sa dérivée par rapport au temps dans [Ra] et dans [R] . - dérivée de : - dérivée de    :    Mais on peut aussi calculer la dérivée de à partir de sa décomposition sur la base étant mobiles dans [Ra]. Il existe donc entre les dérivées de    B.3.1. Référentiels en translation l'un par rapport à l'autre Le mot "translation" signifie que les vecteurs , ont une direction fixe par rapport à il n'y a pas de rotation de [Ra] par rapport à [R]. Pour simplifier nous prendrons les axes respectivement parallèles entre eux : Par suite  :                             Donc:                                  Cette relation est vérifiée chaque fois qu'il n'y a pas rotation des axes les uns par rapport aux autres; mais le mouvement de l'origine O1 du repère [R] peut être quelconque.    B.3.2. [R] animé d'une rotation d'axe Az par rapport à [Ra] Pour simplifier , on supposera les origines des référentiels confondues ainsi que les vecteurs . tournent dans le plan . On repère la position de [R] dans [Ra] par l'angle . On remarque que les vecteurs correspondent aux vecteurs de la base polaire: En reportant dans l'expression (3-1) : Et par suite:   En effet:    B.3.3. 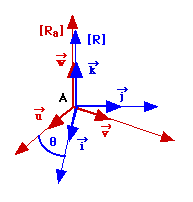[R] en rotation d'axe D par rapport à [Ra] Soient deux référentiels de même origine, [Ra] et [R] , [R] étant en rotation par rapport à [Ra] autour d'un axe D passant par l'origine. La direction de D, qui peut varier au cours du temps, est repérée par un vecteur porté par D. La relation suivante reste valable. La simulation suivante montre la construction des trois composantes du vecteur rotation instantanée lorsque la rotation s'effectue autour d'un axe quelconque variable. 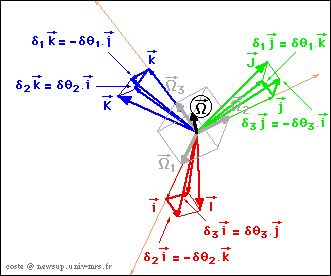Rotations élémentaires   Remarque On note quelquefois différemment les opérateurs de dérivation par rapport à chaque référentiel, ce qui permet d'omettre sans risque d'erreur, les indices dans l'écriture: •  est utilisé pour la dérivation temporelle par rapport à un référentiel considéré comme "fixe" •   est utilisé pour la dérivation temporelle par rapport à un référentiel quelconque, en rotation par rapport au précédent Si les deux référentiels sont en translation : Faire les exercices: Grandeurs cinématiques par rapport à deux référentiels Dérivées de vecteurs par rapport au temps Vitesses et accélérations pour R' en rotation par rapport à R

Mécanique - Chapitre B - 3