|
|
 |
|
|
|
Stigmatisme rigoureux.
Rappel de la figure
Image d'un point sur l'axe:
Le point A1 est pris sur l'axe A1CS et donc son image, si elle existe, sera sur cet axe car le rayon A1CS traverse le dioptre sans être dévié.
Un rayon quelconque A1I se réfracte suivant IA2, les rayons incident, réfracté et la normale au dioptre CI étant situés dans un même plan que l'on choisit comme plan de la figure.
Appliquons la
relation des sinus au triangle ICA1:
puis au triangle
ICA2:
on en déduit: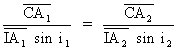 
en tenant compte de la relation: 
on obtient: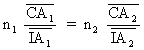 
la quantité:
qui
se conserve à la traversée du dioptre, est un invariant fondamental.
Rappel de la figure
D'autre part:
et 
donc:
soit encore:
d'où:
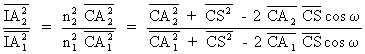
cette relation
montre qu'étant donné le point A1,
CA2 dépend
de 
.
Rappel de la figure
Posons :
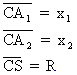La relation précédente s'écrit alors:
Il y aura
stigmatisme
rigoureux si CA2 est indépendant de 
donc si le rapport 
est indépendant de .
on a alors si 
:
et
si 
:
soit
encore:
Rappel de la figure
en appliquant la relation:
on
obtient:
soit encore:
(1) et 
(2)
L'équation (1) a deux solutions possibles:
1) 
les points de la surface du dioptre sont rigoureusement stigmatiques puisque A1 et A2 sont confondus.
ou encore: 
le dioptre présente un stigmatisme rigoureux pour le centre qui est lui-même son propre conjugué.
Rappel de la figure
2)
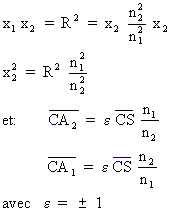
Si n2
> n1 alors
CA1 > R et A1
étant un objet
réel on a 
et
Rappel de la figure
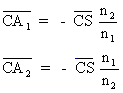
Ces deux points pour lesquels le stigmatisme est rigoureux sont appelés points de Weïerstrass ( ou points d'Young).
Ils sont toujours de nature opposée: si l'un est réel, l'autre est virtuel. Sur chaque diamètre du dioptre existe un couple de tels points.
Soient W1 et W2 les points objet et image de Weïerstrass. On a alors:
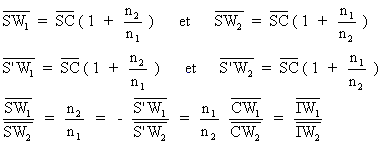
Les quatre points W1, S', W2 et S forment une division harmonique et le lieu des points I tels que le rapport IW1/IW2 soit constant est la sphère de diamètre SS'.
Si n1>n2, alors A1 est entre C et S', A2 est extérieur à SS'; par contre, si n1<n2, alors A1 est extérieur à SS' et A2 est entre C et S'.
L'animation suivante illustre les propriétés de stigmatisme du dioptre sphérique:
|
|
|
