|
|
 |
|
|
|
Equation fondamentale
Rappel de la figure
Soit un miroir sphérique de centre C et de sommet S. Appelons A un point lumineux quelconque de l'espace; celui-ci est contenu dans un plan de section principale que l'on prend comme plan de figure.
Considérons un rayon incident quelconque AI qui après réflexion se propage suivant IR. Si le miroir donne de A une image A' celle-ci est nécessairement au point d'intersection de IR avec le rayon lumineux AC, qui se réfléchit sur lui-même puisqu'il est normal au miroir (axe secondaire).
Traçons la tangente IT au point d'incidence I; nous observons que les deux droites IC et IT ne sont autres que les deux bissectrices de l'angle AIA', c'est-à-dire que les quatre points A, A', C et T forment une division harmonique
Dans le triangle CAI on a la relation:
soit: 
et dans le triangle CA'I la relation:
d'où: 
Rappel de la figure
On en déduit la relation: 
dans le triangle TAI on a la relation:
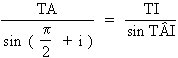on en déduit: 
et dans le triangle TA'I: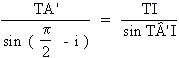 
d'où:
soit: 
Des relations précédentes on déduit: 
soit: 
si on rapporte toutes les grandeurs algébriques à une même origine, le centre C du miroir. On note par ailleurs que:
; en désignant par:
- r le rayon de courbure du miroir
- 
Rappel de la figure
On a donc finalement:
|
Cette relation représente l'équation fondamentale des miroirs sphériques.
|
|
|
