|
La construction de Fresnel permet de représenter une grandeur sinusoïdale par un vecteur tournant. A chaque instant la grandeur sera égale à la projection du vecteur qui la représente sur l'axe de référence.
Exemple :
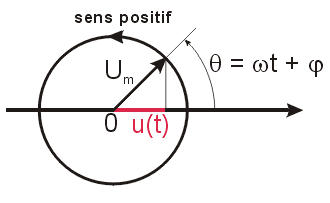
une tension u(t) = Umcos (wt + j) sera représentée par un vecteur :
- de longueur proportionnelle à Um,
- tournant à la vitesse angulaire w,
- faisant à l'instant t = 0 un angle j avec l'axe choisi comme origine des phases (axe de référence)
Remarque 1 :
Si l'on représente sur la même construction de Fresnel plusieurs tensions de même fréquence, les vecteurs qui les représentent tournent à la même vitesse. La figure obtenue tourne donc sans se déformer.
Par commodité, on choisit de la construire à t = 0. Dans ce cas, pour représenter une tension, il suffira de construire un vecteur de longueur proportionnelle à Um faisant un angle j avec l'axe choisi comme origine des phases. Toute tension sera ainsi associée à un point du plan.
Remarque 2 :
La construction de Fresnel est surtout commode pour l'étude des associations de dipôles en série. Comme ils sont parcourus par le même courant, on prendra comme origine des phases le vecteur représentant l'intensité. Le vecteur représentant une somme de tensions sera obtenu en construisant la somme des vecteurs représentant les tensions à additionner.