Utilisation des nombres complexes

Au lieu de repérer un point du plan en définissant le vecteur joignant ce point à l'origine, comme dans la construction de Fresnel, on peut le repérer par un nombre complexe Z = a + jb = r.e^jq ; la première notation est l'équivalent, en notation complexe, des coordonnées cartésiennes, la seconde l'équivalent des coordonnées polaires. De même que dans la construction de Fresnel, la tension est égale à la projection du vecteur sur l'axe de référence, ici la tension est égale à la partie réelle du nombre complexe qui la représente.

Exemple :

Une tension u(t) = U_mcos (wt + j) sera représentée par un nombre complexe :

comme : e^jq = cos q + j.sin q
si on pose : q = (wt + j)
on a bien : ; est la partie réelle de
On peut aussi écrire:

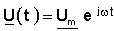
est appelé "amplitude complexe" de la tension