de lois de vitesse
d'ordre simple
d'ordre 0
| Chapitre 2 | Approche formelle de lois de vitesse d'ordre simple |
Réaction d'ordre 0 |
2.1 Réactions
d'ordre 0.
Loi de vitesse.
La vitesse des réactions d'ordre
0 est constante. Cette vitesse se maintient tant qu'il reste du réactif.
| La loi de
vitesse |
|
|
|
k en mol.l-1.s-1 |
|
C0
étant la concentration initiale du réactif |
|
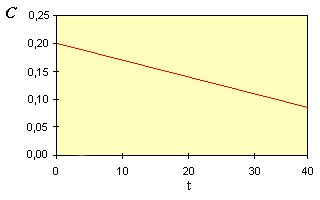 |
| La représentation graphique de C = f(t) est une droite de pente - k. |
Temps de demi-vie.
Le temps de demi-vie ![]() est proportionnel à
la concentration initiale. Il est égal
à :
est proportionnel à
la concentration initiale. Il est égal
à :
Vérification
de l'ordre.
En portant sur un graphique la concentration
C en fonction du temps, on doit obtenir une droite de pente - k.
Les valeurs du coefficient de
vitesse k calculées pour chaque mesure expérimentale par la
loi d'ordre 0 : ![]() doivent être sensiblement
constantes.
doivent être sensiblement
constantes.
| Chapitre 2 | Approche formelle de lois de vitesse d'ordre simple |
Réactions d'ordre un |
1.2
Réaction d'ordre 1.
Loi de vitesse.
La vitesse est d'une
réaction d'ordre un est proportionnelle à la concentration du réactif
: ![]()
qui s'intègre en :
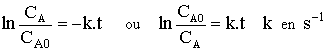 |
CA0 étant la concentration initiale de A et CA sa concentration au temps t.
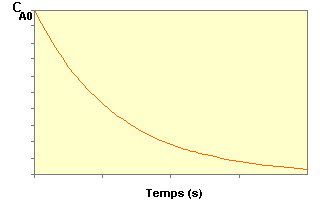
La variation
de CA au cours du temps suit une courbe de
décroissance exponentielle : ![]()
Temps
de demi-vie.
Le temps de demi-vie ![]() est indépendant de la concentration initiale. C'est
un caractéristique des réactions d'ordre un.
est indépendant de la concentration initiale. C'est
un caractéristique des réactions d'ordre un.
Vérification de l'ordre 1 d'une réaction.
On peut s'assurer qu'une réaction
obéit bien à une loi du premier ordre en vérifiant l'une ou l'autre des
relations suivantes :
| Chapitre 2 | Approche formelle de lois de vitesse d'ordre simple |
Réactions d'ordre global deux |
2.3
Réaction d'ordre global 2 :
Réactions qui obéissent à une loi
de vitesse ![]() ou
ou ![]()
suivant que l'ordre est 2 par rapport à un réactif
ou que l'on a un ordre partiel 1 pour deux réactifs.
| Réactions
d'ordre global deux |
Ordre
2 par rapport à un seul réactif |
2.3.1
Ordre 2 par rapport à un seul réactif.
Loi de vitesse
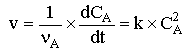
qui s'intègre en
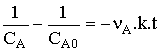
Dans le cas usuel où le coefficient stoechiométrique vaut 2: nA = - 2 d'où
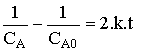 ( k en L mol-1 s-1 )
( k en L mol-1 s-1 ) |
La variation de CA au cours du temps est représentée sur la figure ci-dessous :
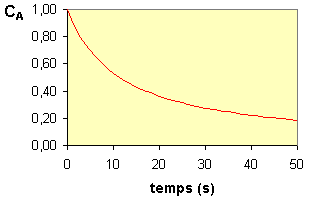
Temps de demi-vie.
Le temps de demi-vie d'une réaction
d'ordre deux est inversement proportionnel à la concentration.
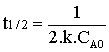 |
Vérification de l'ordre 2.
On peut s'assurer qu'une réaction obéit bien à une loi du second ordre en vérifiant l'une ou l'autre des relations suivantes :
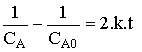
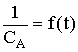 qui doit donner une droite.
qui doit donner une droite. | Réactions
d'ordre global deux |
Ordre partiel
1 par rapport à deux réactifs |
2.3.2 Ordre partiel 1 par rapport à deux réactifs.
Cas des réactions
du type : A +
B = Produits avec ![]()
Cas
particuler pour lequel les concentrations initiales sont égales,
CA0
= CB0 les
concentrations au cours du temps restent alors égales CA = CB et la
loi de vitesse est la même que précédemment : ![]() d'où
la même expression intégrée.
d'où
la même expression intégrée.
A savoir :
k en L mol-1 s-1
Lorsque les concentrations initiales sont différentes : CA0 différent de CB0
La loi de vitesse sous sa forme différentielle 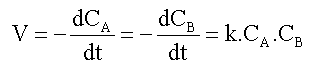 s'intègre
en
s'intègre
en 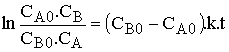
| Chapitre 2 | Approche formelle de lois de vitesse d'ordre simple |
Fin |